数据结构 - 线性结构 - 队列(Queue)

队列(Queue) 是一种抽象的线性数据结构，其核心约束只有一句话 —— 先入先出。

1 队列

队列 (Queue) 是一种遵循先入先出规则的线性数据结构。顾名思义，队列模拟了排队现象，即新来的人不断加入队列尾部，而位于队列头部的人逐个离开。

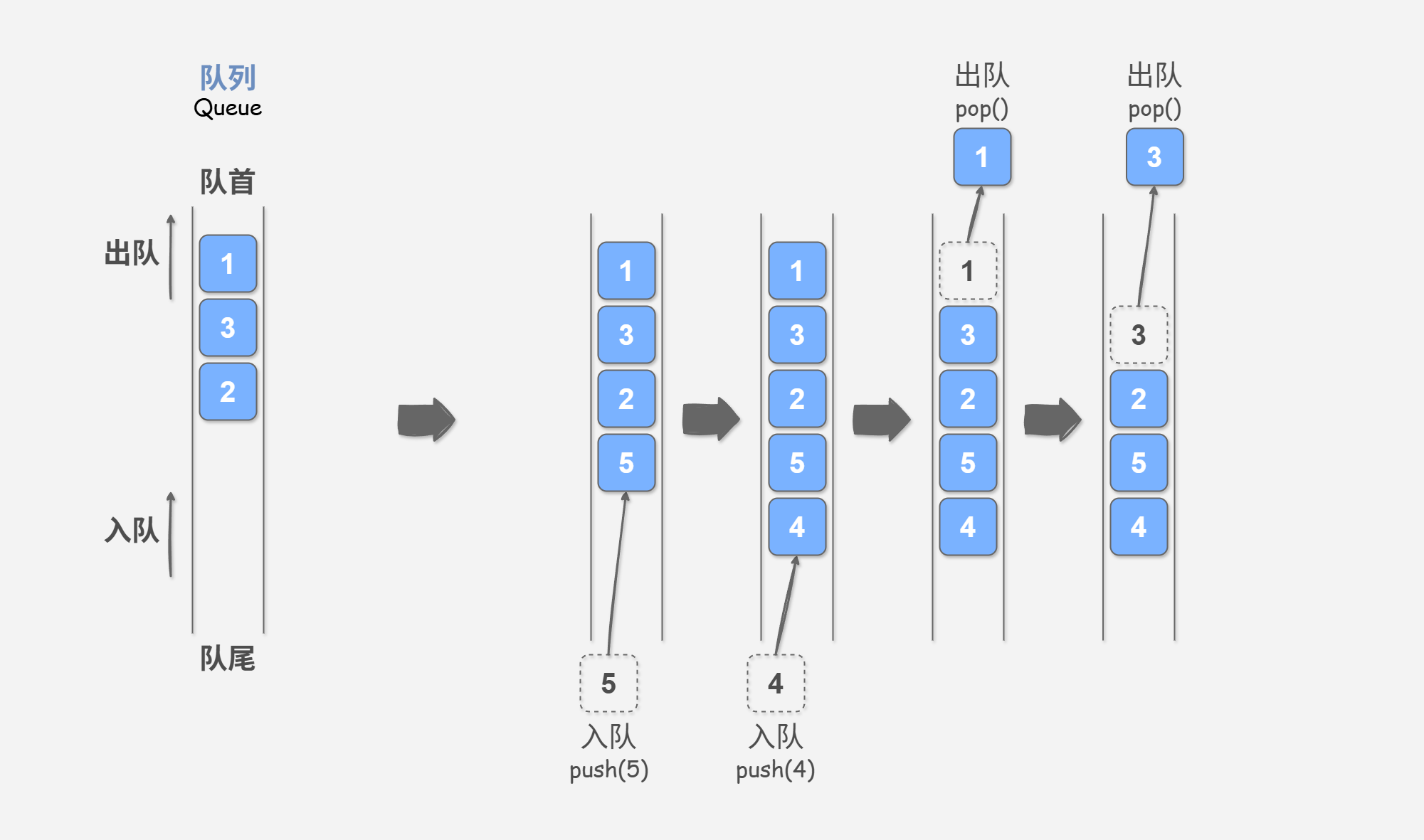
如 图 1-1 所示，我们将队列头部称为“队首”，尾部称为“队尾”，将把元素加入队尾的操作称为“入队”，删除队首元素的操作称为“出队”。

图 1-1 队列的先入先出规则

1.1 队列常用操作

队列的常见操作如下表所示。需要注意的是，不同编程语言的方法名称可能会有所不同。我们在此采用与栈相同的方法命名。

方法名	描述	时间复杂度
push()	元素入队，即将元素添加至队尾	$O(1)$
pop()	队首元素出队	$O(1)$
peek()	访问队首元素	$O(1)$

1	// C 未提供内置队列

from collections import deque

# 初始化队列
# 在 Python 中，我们一般将双向队列类 deque 当作队列使用
# 虽然 queue.Queue() 是纯正的队列类，但不太好用，因此不推荐
que: deque[int] = deque()

# 元素入队
que.append(1)
que.append(3)
que.append(2)
que.append(5)
que.append(4)

# 访问队首元素
front: int = que[0]

# 元素出队
pop: int = que.popleft()

# 获取队列的长度
size: int = len(que)

# 判断队列是否为空
is_empty: bool = len(que) == 0

2 队列实现

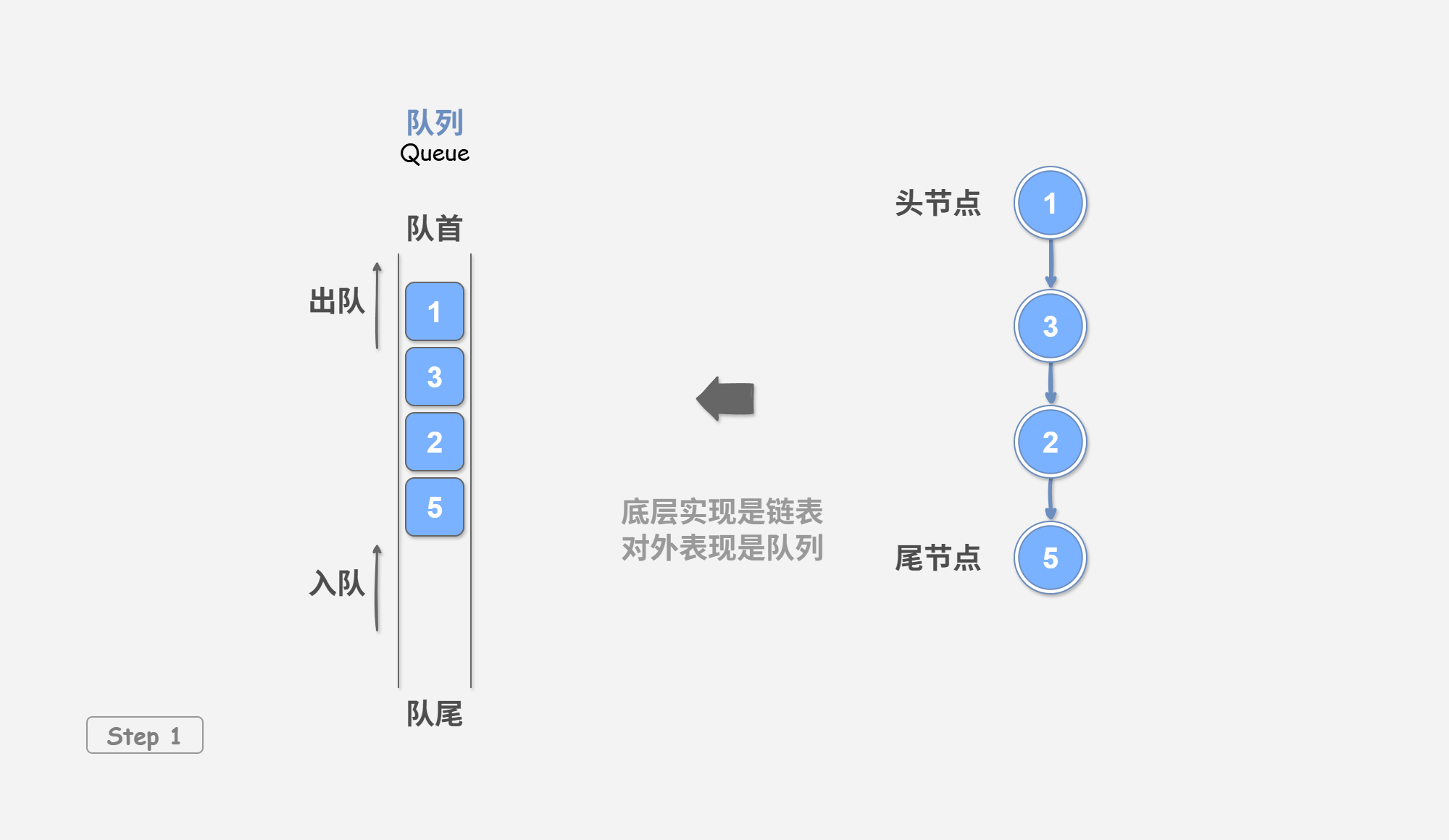
为了实现队列，我们需要一种数据结构，可以在一端添加元素，并在另一端删除元素，链表和数组都符合要求。

2.1 基于链表的实现

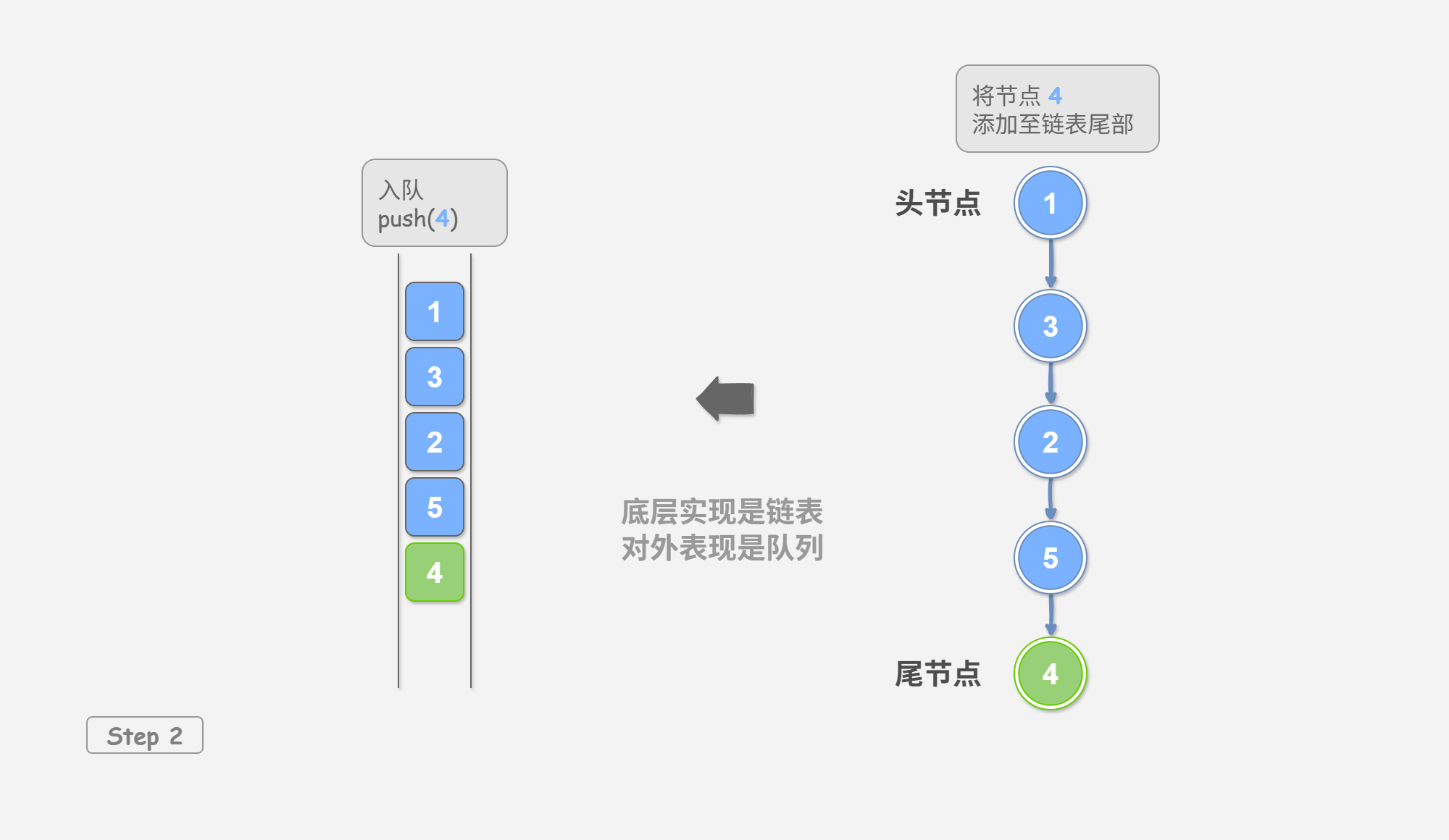
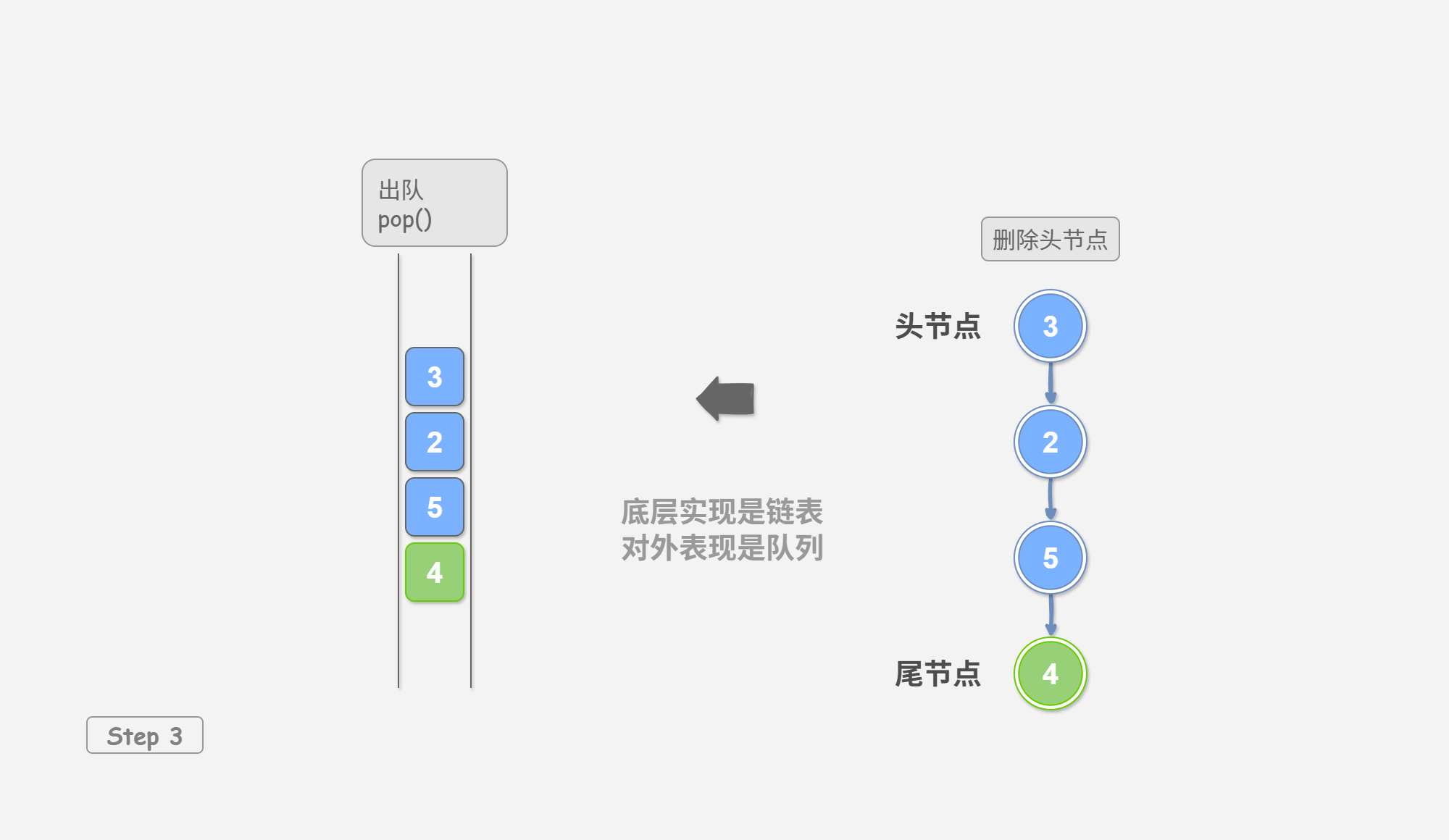
如 图 2-1 所示，我们可以将链表的“头节点”和“尾节点”分别视为“队首”和“队尾”，规定队尾仅可添加节点，队首仅可删除节点。

LinkedListQueue

push()

pop()

图 2-1 基于链表实现队列的入队出队操作

一下是用链表实现队列的代码：

Python

/* 基于链表实现的队列 */
typedef struct {
    ListNode *front, *rear;
    int queSize;
} LinkedListQueue;

/* 构造函数 */
LinkedListQueue *newLinkedListQueue() {
    LinkedListQueue *queue = (LinkedListQueue *)malloc(sizeof(LinkedListQueue));
    queue->front = NULL;
    queue->rear = NULL;
    queue->queSize = 0;
    return queue;
}

/* 析构函数 */
void delLinkedListQueue(LinkedListQueue *queue) {
    // 释放所有节点
    while (queue->front != NULL) {
        ListNode *tmp = queue->front;
        queue->front = queue->front->next;
        free(tmp);
    }
    // 释放 queue 结构体
    free(queue);
}

/* 获取队列的长度 */
int size(LinkedListQueue *queue) {
    return queue->queSize;
}

/* 判断队列是否为空 */
bool empty(LinkedListQueue *queue) {
    return (size(queue) == 0);
}

/* 入队 */
void push(LinkedListQueue *queue, int num) {
    // 尾节点处添加 node
    ListNode *node = newListNode(num);
    // 如果队列为空，则令头、尾节点都指向该节点
    if (queue->front == NULL) {
        queue->front = node;
        queue->rear = node;
    }
    // 如果队列不为空，则将该节点添加到尾节点后
    else {
        queue->rear->next = node;
        queue->rear = node;
    }
    queue->queSize++;
}

/* 访问队首元素 */
int peek(LinkedListQueue *queue) {
    assert(size(queue) && queue->front);
    return queue->front->val;
}

/* 出队 */
int pop(LinkedListQueue *queue) {
    int num = peek(queue);
    ListNode *tmp = queue->front;
    queue->front = queue->front->next;
    free(tmp);
    queue->queSize--;
    return num;
}

/* 打印队列 */
void printLinkedListQueue(LinkedListQueue *queue) {
    int *arr = malloc(sizeof(int) * queue->queSize);
    // 拷贝链表中的数据到数组
    int i;
    ListNode *node;
    for (i = 0, node = queue->front; i < queue->queSize; i++) {
        arr[i] = node->val;
        node = node->next;
    }
    printArray(arr, queue->queSize);
    free(arr);
}

class LinkedListQueue:
    """基于链表实现的队列"""

    def __init__(self):
        """构造方法"""
        self._front: ListNode | None = None  # 头节点 front
        self._rear: ListNode | None = None  # 尾节点 rear
        self._size: int = 0

    def size(self) -> int:
        """获取队列的长度"""
        return self._size

    def is_empty(self) -> bool:
        """判断队列是否为空"""
        return self._size == 0

    def push(self, num: int):
        """入队"""
        # 在尾节点后添加 num
        node = ListNode(num)
        # 如果队列为空，则令头、尾节点都指向该节点
        if self._front is None:
            self._front = node
            self._rear = node
        # 如果队列不为空，则将该节点添加到尾节点后
        else:
            self._rear.next = node
            self._rear = node
        self._size += 1

    def pop(self) -> int:
        """出队"""
        num = self.peek()
        # 删除头节点
        self._front = self._front.next
        self._size -= 1
        return num

    def peek(self) -> int:
        """访问队首元素"""
        if self.is_empty():
            raise IndexError("队列为空")
        return self._front.val

    def to_list(self) -> list[int]:
        """转化为列表用于打印"""
        queue = []
        temp = self._front
        while temp:
            queue.append(temp.val)
            temp = temp.next
        return queue

2.2 基于数组的实现

在数组中删除首元素的时间复杂度为 $O(n)$ ，这会导致出队操作效率较低。然而，我们可以采用一下巧妙的方法来避免这个问题。

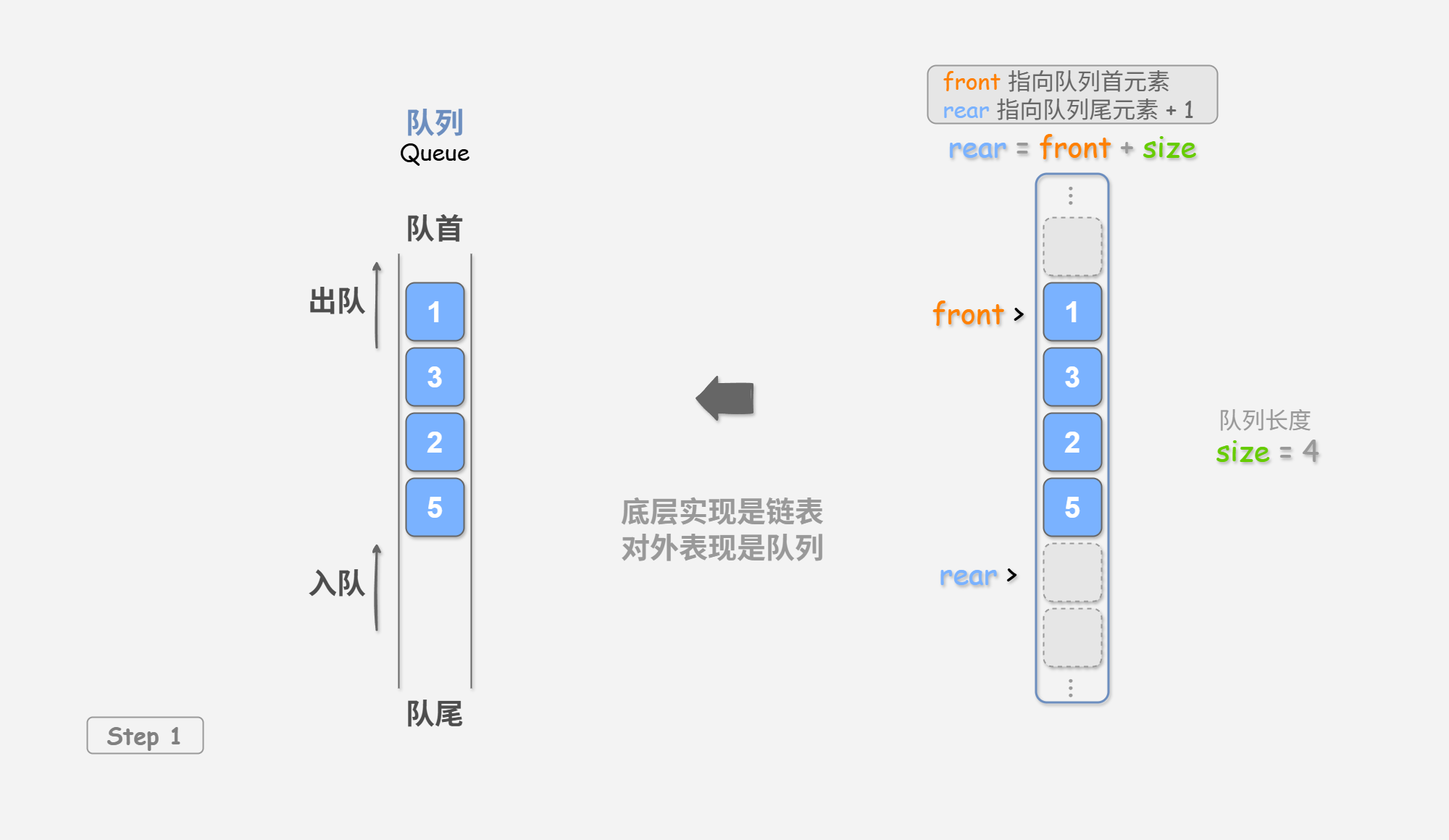
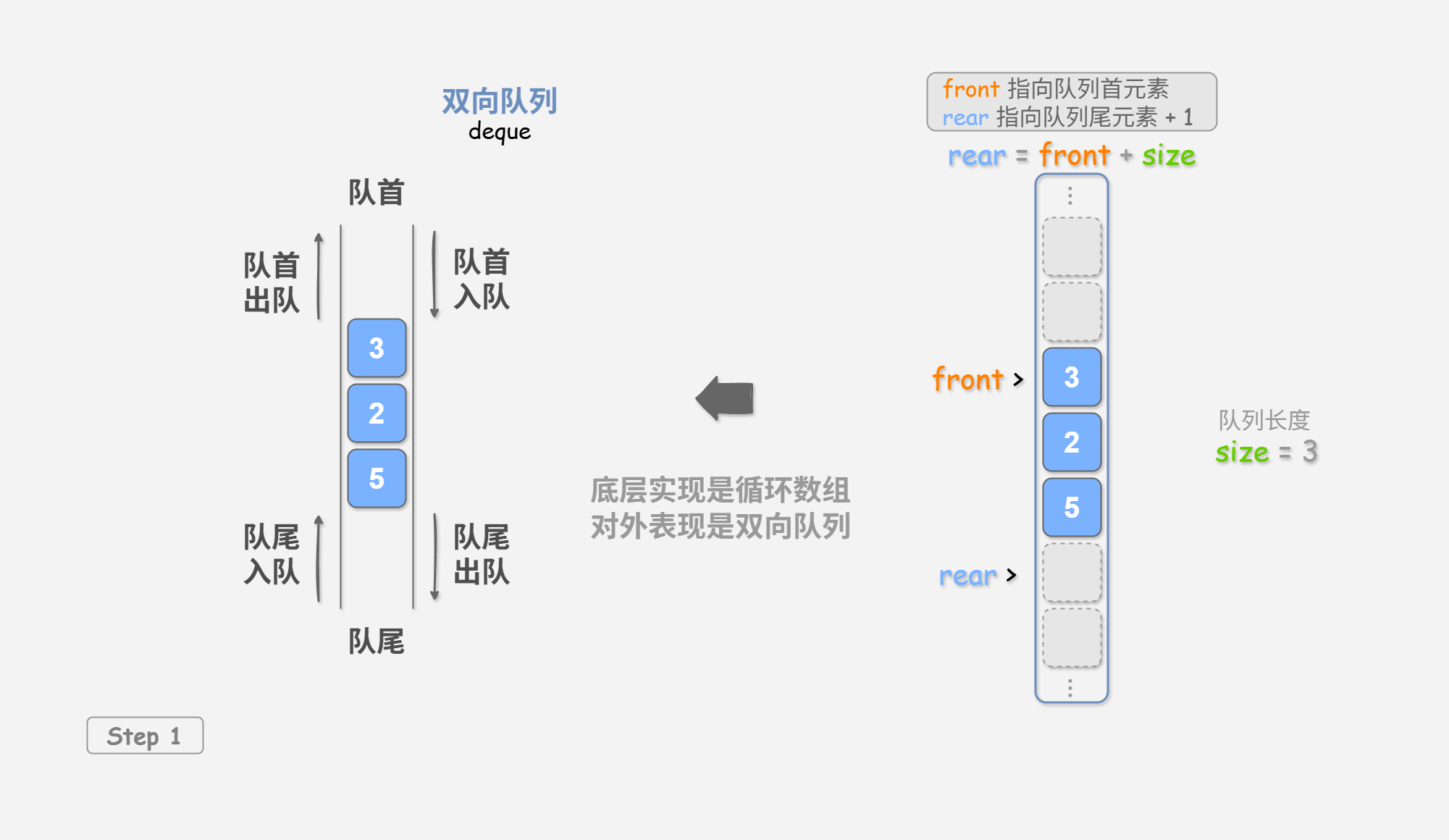
我们可以使用一个变量 front 指向队首元素的索引，并维护一个变量 size 用于记录队列长度。定义 rear = front + size ，这个公式计算出的 rear 指向队尾元素之后的下一个位置。

基于此设计，数组中包含元素的有效区间为 [front, rear - 1] ，各种操作的实现方法如 图 3-2 所示。

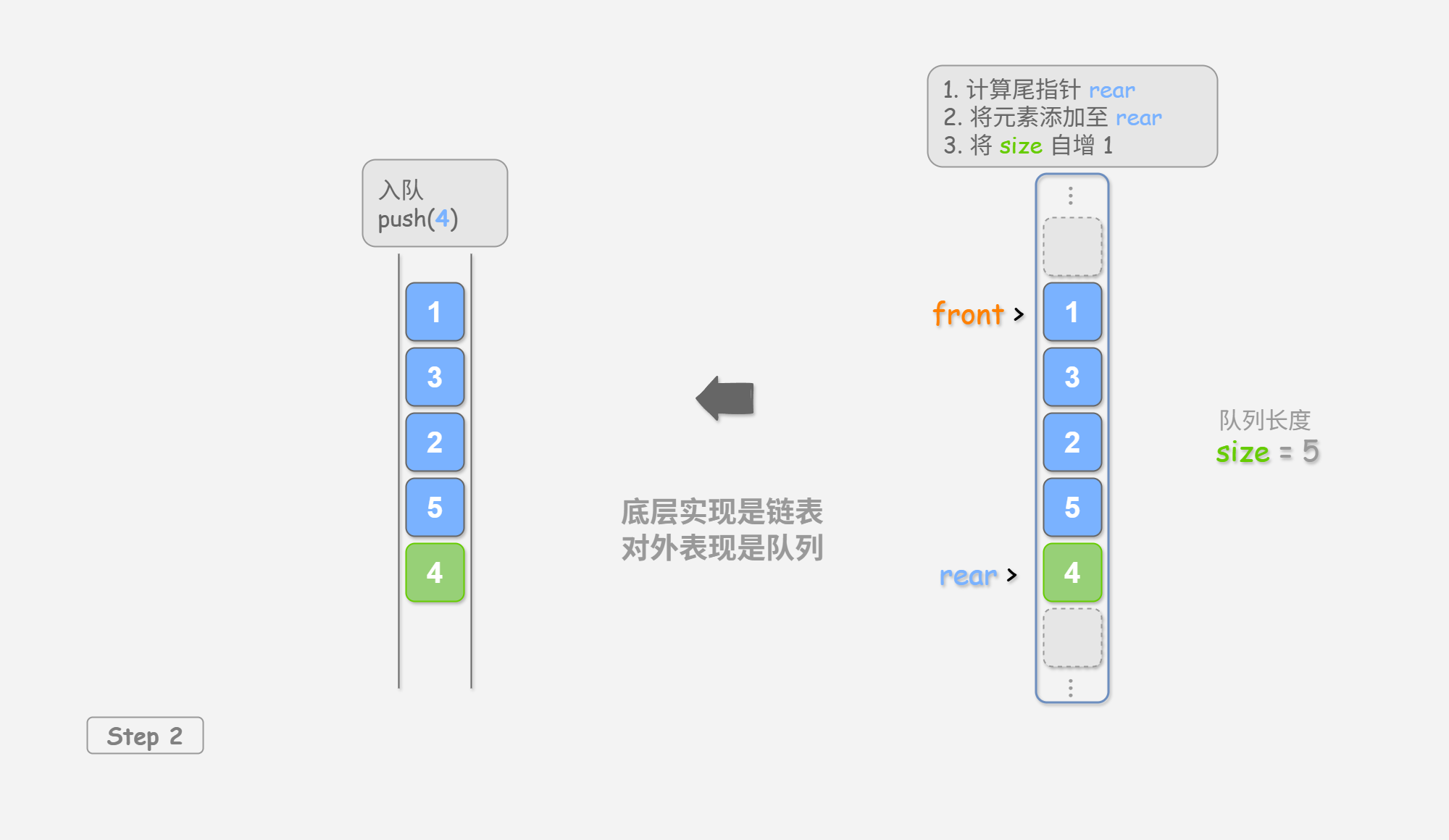
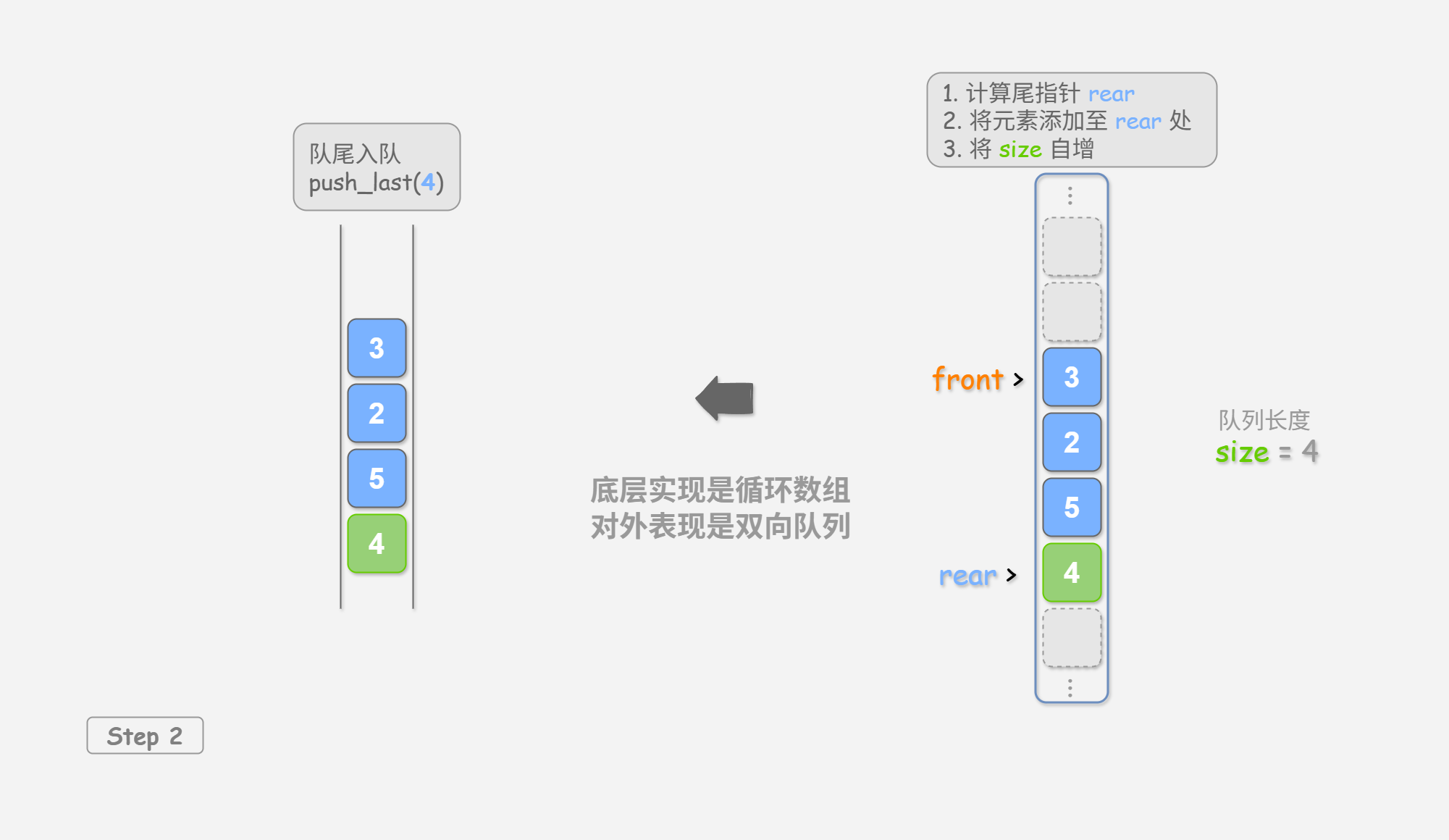
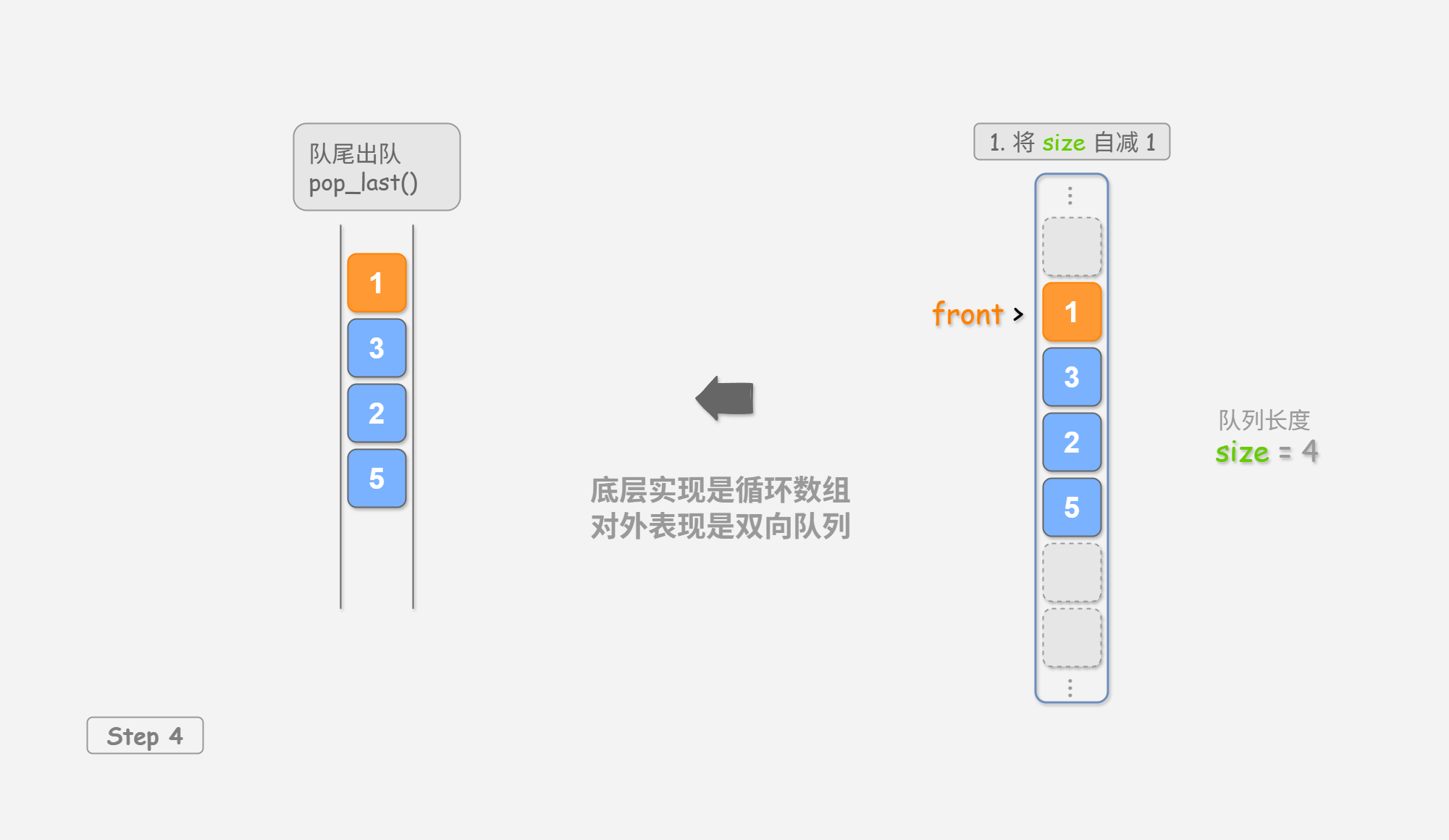
入队操作：将输入元素赋值给 rear 索引处，并将 size 增加 1 。
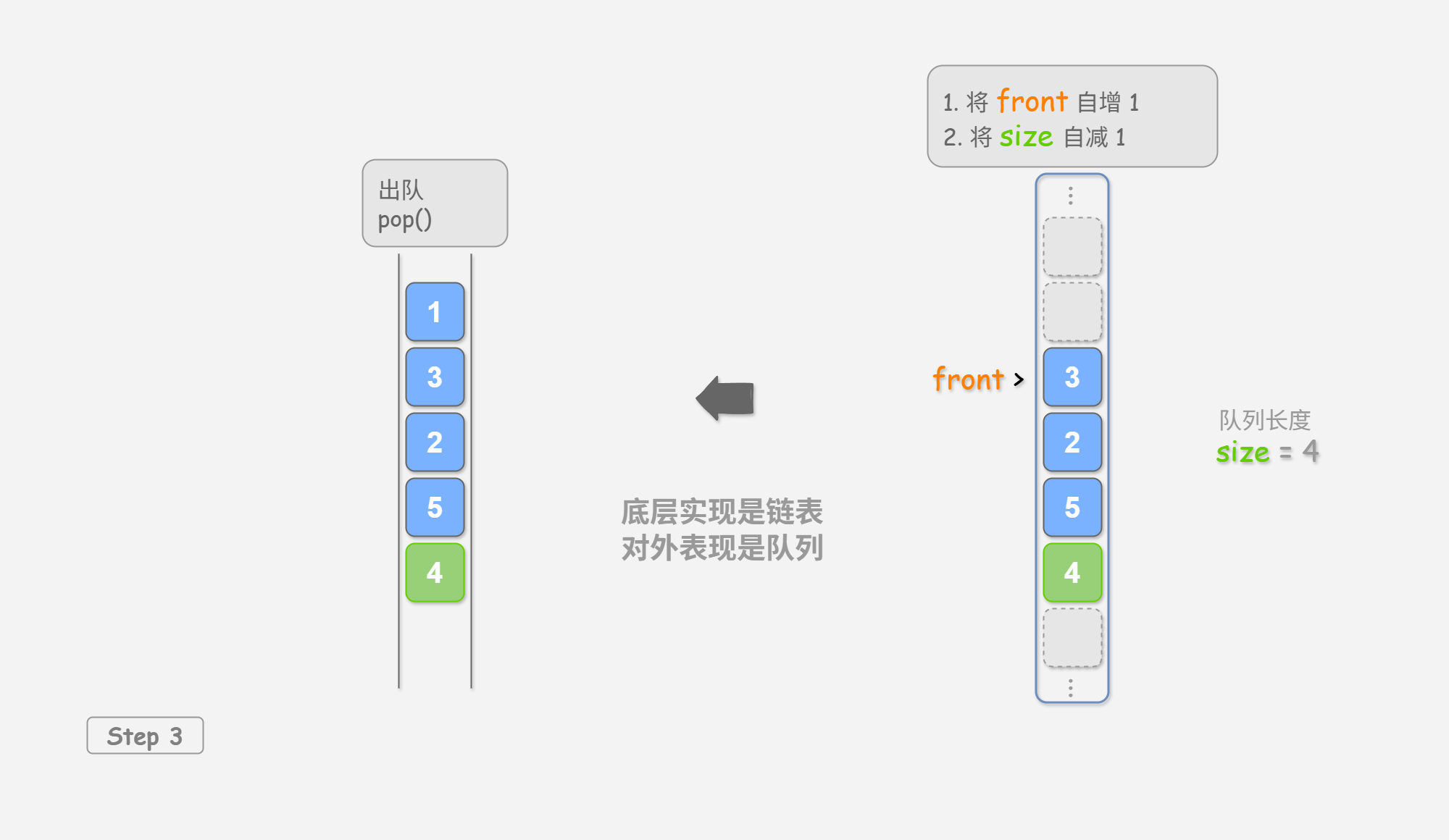
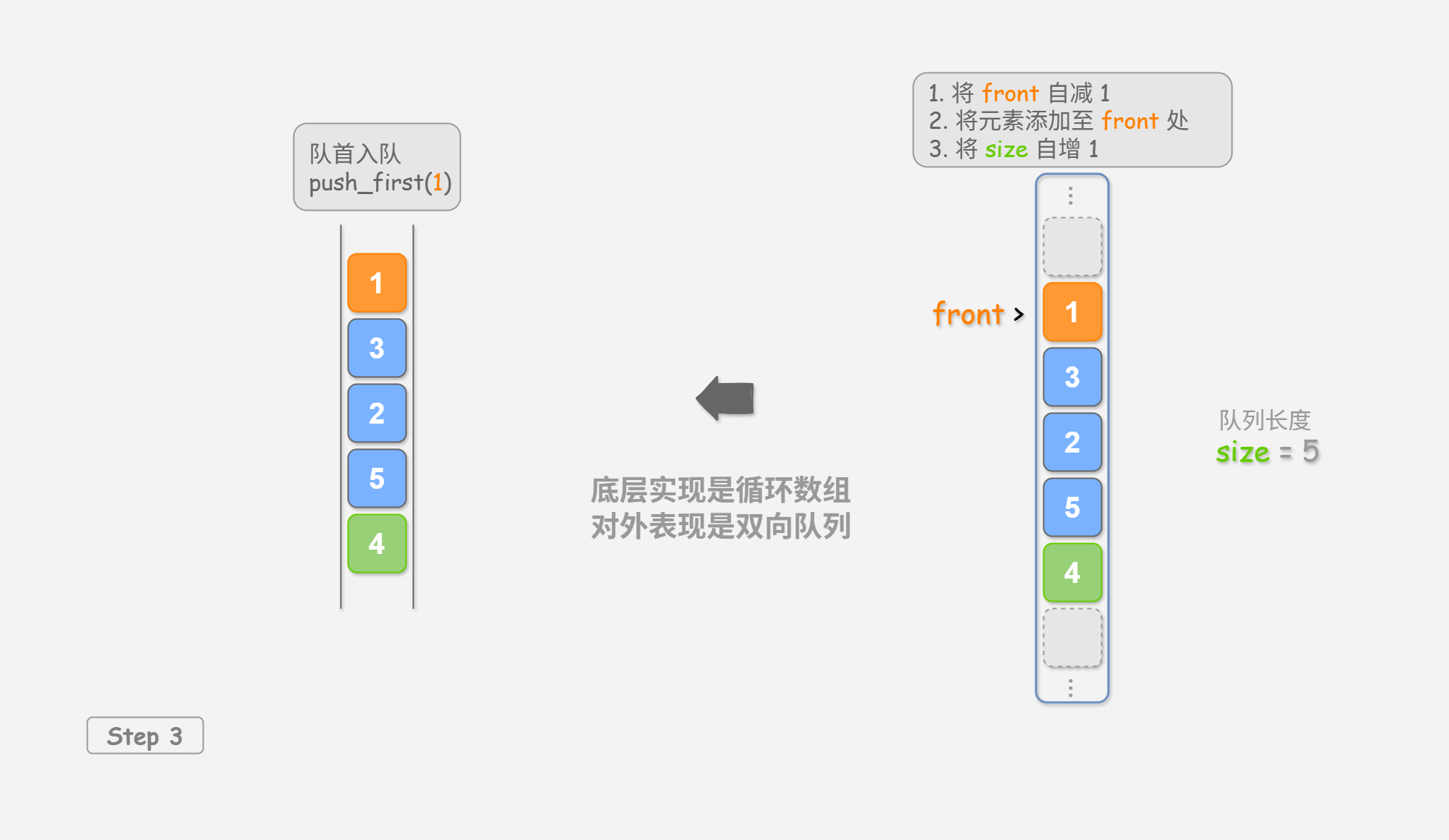
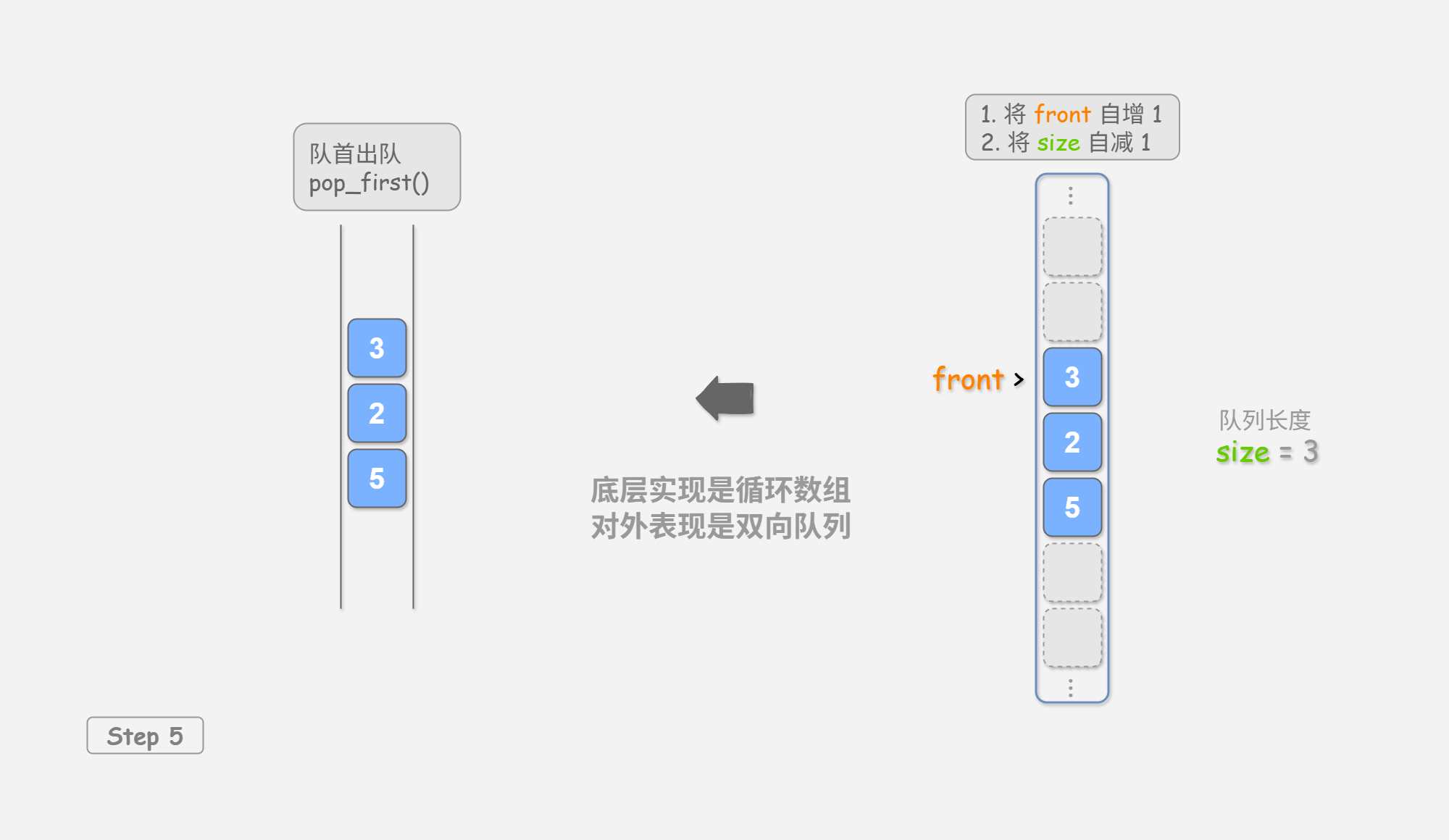
出队操作：只需将 front 增加 1 ，并将 size 减少 1 。

可以看到，入队和出队操作都只需进行一次操作，时间复杂度均为 $O(1)$ 。

ArrayQueue

push()

pop()

图 2-2 基于数组实现队列的入队出队操作

你可能会发现一个问题：在不断进行入队和出队的过程中， front 和 rear 都在向右移动，当他们到达数组尾部时就无法继续移动了。为了解决此问题，我们可以将数组视为首尾相接的“环形数组”。

对于环形数组，我们需要让 front 或 rear 在越过数组尾部时，直接回到数组头部继续遍历。这种周期性规律可以通过“取余操作”来实现，代码如下所示：

Python

/* 基于环形数组实现的队列 */
typedef struct {
    int *nums;       // 用于存储队列元素的数组
    int front;       // 队首指针，指向队首元素
    int queSize;     // 尾指针，指向队尾 + 1
    int queCapacity; // 队列容量
} ArrayQueue;

/* 构造函数 */
ArrayQueue *newArrayQueue(int capacity) {
    ArrayQueue *queue = (ArrayQueue *)malloc(sizeof(ArrayQueue));
    // 初始化数组
    queue->queCapacity = capacity;
    queue->nums = (int *)malloc(sizeof(int) * queue->queCapacity);
    queue->front = queue->queSize = 0;
    return queue;
}

/* 析构函数 */
void delArrayQueue(ArrayQueue *queue) {
    free(queue->nums);
    free(queue);
}

/* 获取队列的容量 */
int capacity(ArrayQueue *queue) {
    return queue->queCapacity;
}

/* 获取队列的长度 */
int size(ArrayQueue *queue) {
    return queue->queSize;
}

/* 判断队列是否为空 */
bool empty(ArrayQueue *queue) {
    return queue->queSize == 0;
}

/* 访问队首元素 */
int peek(ArrayQueue *queue) {
    assert(size(queue) != 0);
    return queue->nums[queue->front];
}

/* 入队 */
void push(ArrayQueue *queue, int num) {
    if (size(queue) == capacity(queue)) {
        printf("队列已满\r\n");
        return;
    }
    // 计算队尾指针，指向队尾索引 + 1
    // 通过取余操作实现 rear 越过数组尾部后回到头部
    int rear = (queue->front + queue->queSize) % queue->queCapacity;
    // 将 num 添加至队尾
    queue->nums[rear] = num;
    queue->queSize++;
}

/* 出队 */
int pop(ArrayQueue *queue) {
    int num = peek(queue);
    // 队首指针向后移动一位，若越过尾部，则返回到数组头部
    queue->front = (queue->front + 1) % queue->queCapacity;
    queue->queSize--;
    return num;
}

/* 返回数组用于打印 */
int *toArray(ArrayQueue *queue, int *queSize) {
    *queSize = queue->queSize;
    int *res = (int *)calloc(queue->queSize, sizeof(int));
    int j = queue->front;
    for (int i = 0; i < queue->queSize; i++) {
        res[i] = queue->nums[j % queue->queCapacity];
        j++;
    }
    return res;
}

class ArrayQueue:
    """基于环形数组实现的队列"""

    def __init__(self, size: int):
        """构造方法"""
        self._nums: list[int] = [0] * size  # 用于存储队列元素的数组
        self._front: int = 0  # 队首指针，指向队首元素
        self._size: int = 0  # 队列长度

    def capacity(self) -> int:
        """获取队列的容量"""
        return len(self._nums)

    def size(self) -> int:
        """获取队列的长度"""
        return self._size

    def is_empty(self) -> bool:
        """判断队列是否为空"""
        return self._size == 0

    def push(self, num: int):
        """入队"""
        if self._size == self.capacity():
            raise IndexError("队列已满")
        # 计算队尾指针，指向队尾索引 + 1
        # 通过取余操作实现 rear 越过数组尾部后回到头部
        rear: int = (self._front + self._size) % self.capacity()
        # 将 num 添加至队尾
        self._nums[rear] = num
        self._size += 1

    def pop(self) -> int:
        """出队"""
        num: int = self.peek()
        # 队首指针向后移动一位，若越过尾部，则返回到数组头部
        self._front = (self._front + 1) % self.capacity()
        self._size -= 1
        return num

    def peek(self) -> int:
        """访问队首元素"""
        if self.is_empty():
            raise IndexError("队列为空")
        return self._nums[self._front]

    def to_list(self) -> list[int]:
        """返回列表用于打印"""
        res = [0] * self.size()
        j: int = self._front
        for i in range(self.size()):
            res[i] = self._nums[(j % self.capacity())]
            j += 1
        return res

以上实现的队列仍然具有局限性：其长度不可变。然而，这个问题不难解决，我们可以将数组替换为动态数组，从而引入扩容机制。有兴趣的读者可以尝试自行实现。两种实现的对比结论与栈一致，在此不再赘述。

注意

一般，在嵌入式，或者说在固件、裸机里尽量不使用动态数组。

3 双向队列

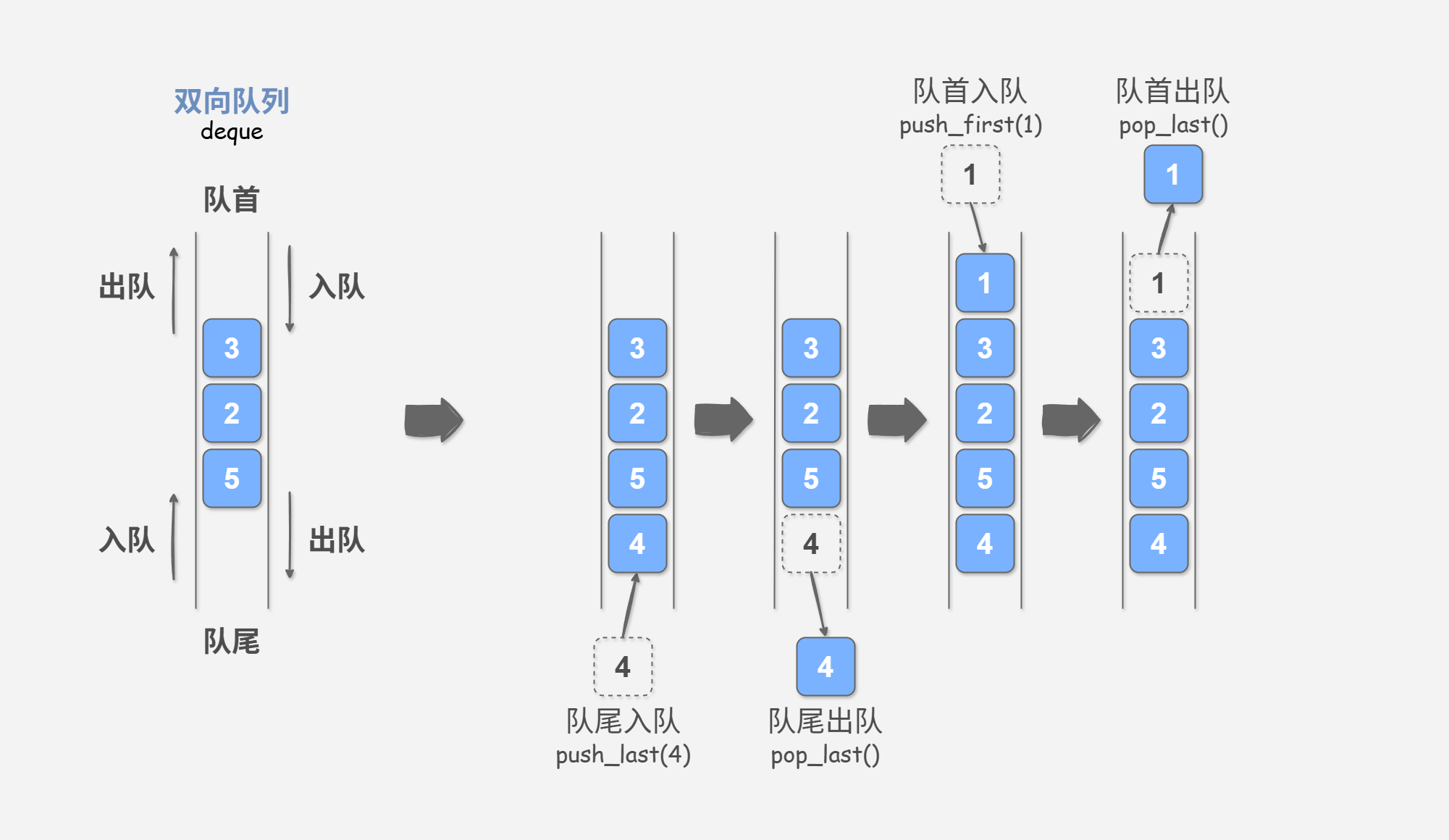
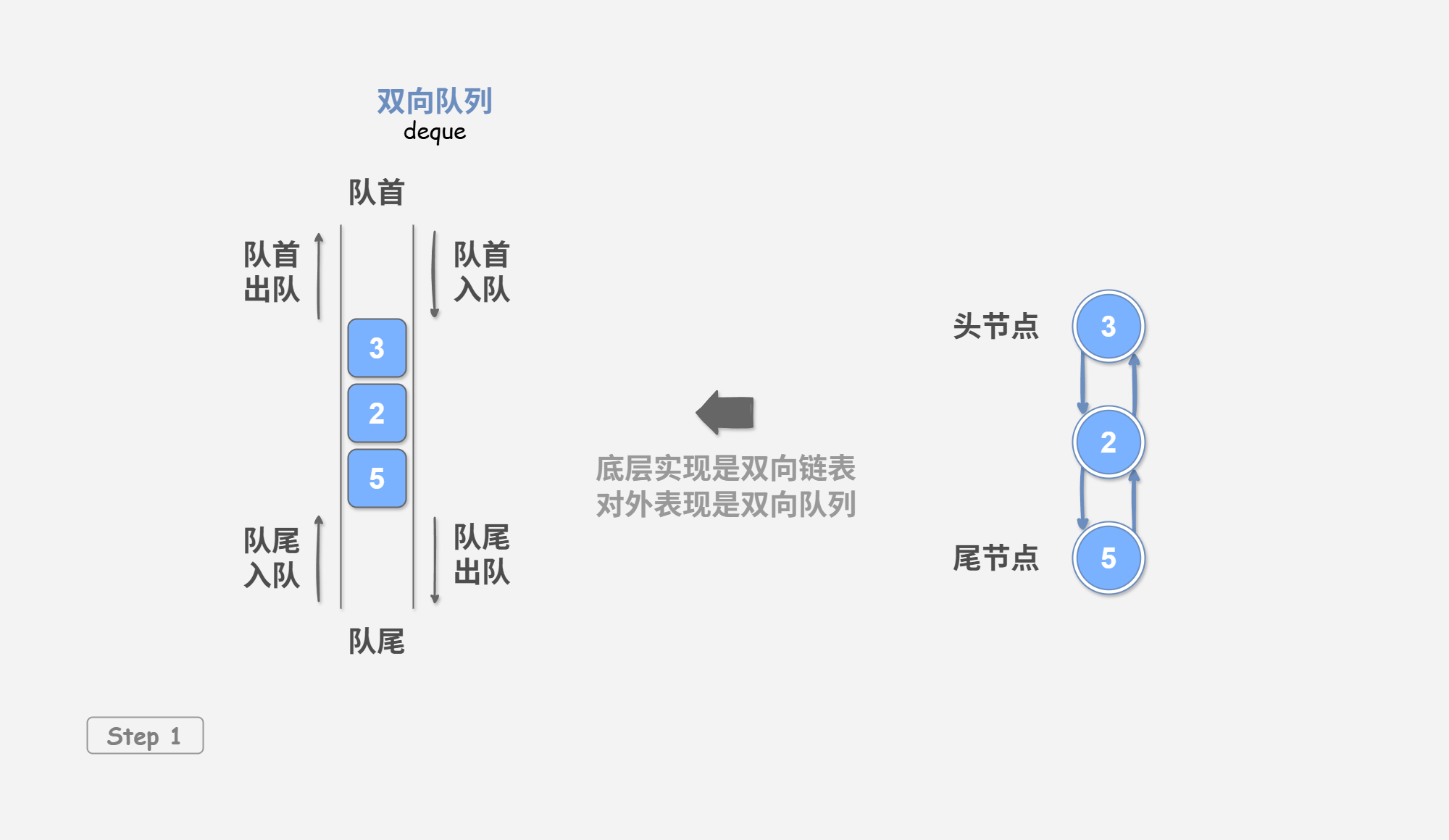
在队列中，我们仅能删除头部元素或在尾部添加元素。双向队列 (double-ended queue) 如 图 3-1 所示，提供了更高的灵活性，允许在头部和尾部执行元素的添加或删除操作。

图 3-1 双向队列的操作

3.1 双向队列常用操作

双向队列的常用操作如下表所示，具体的方法名称需要根据所使用的编程语言来确定。

方法名	描述	时间复杂度
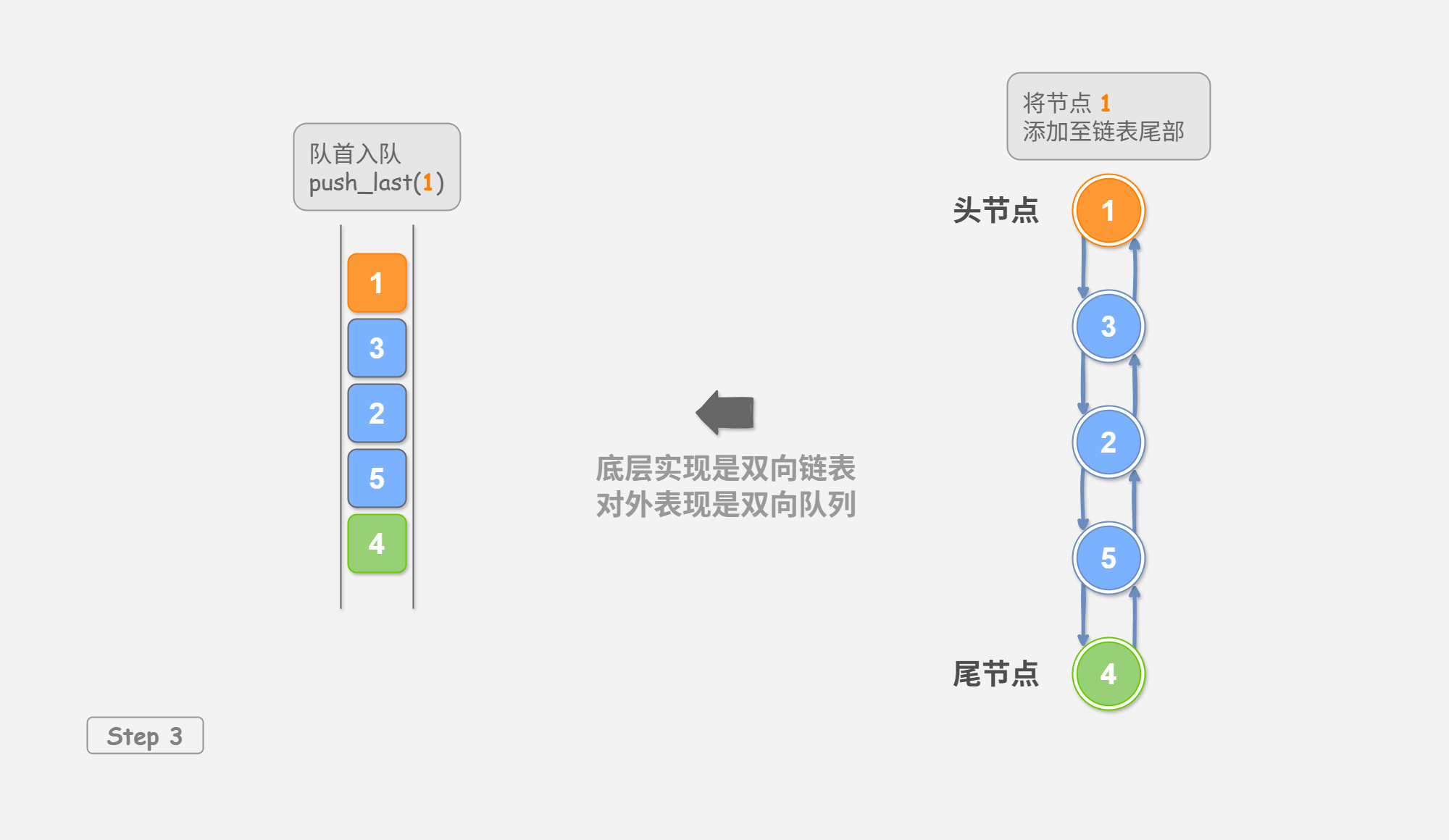
push_first()	将元素添加至队首	$O(1)$
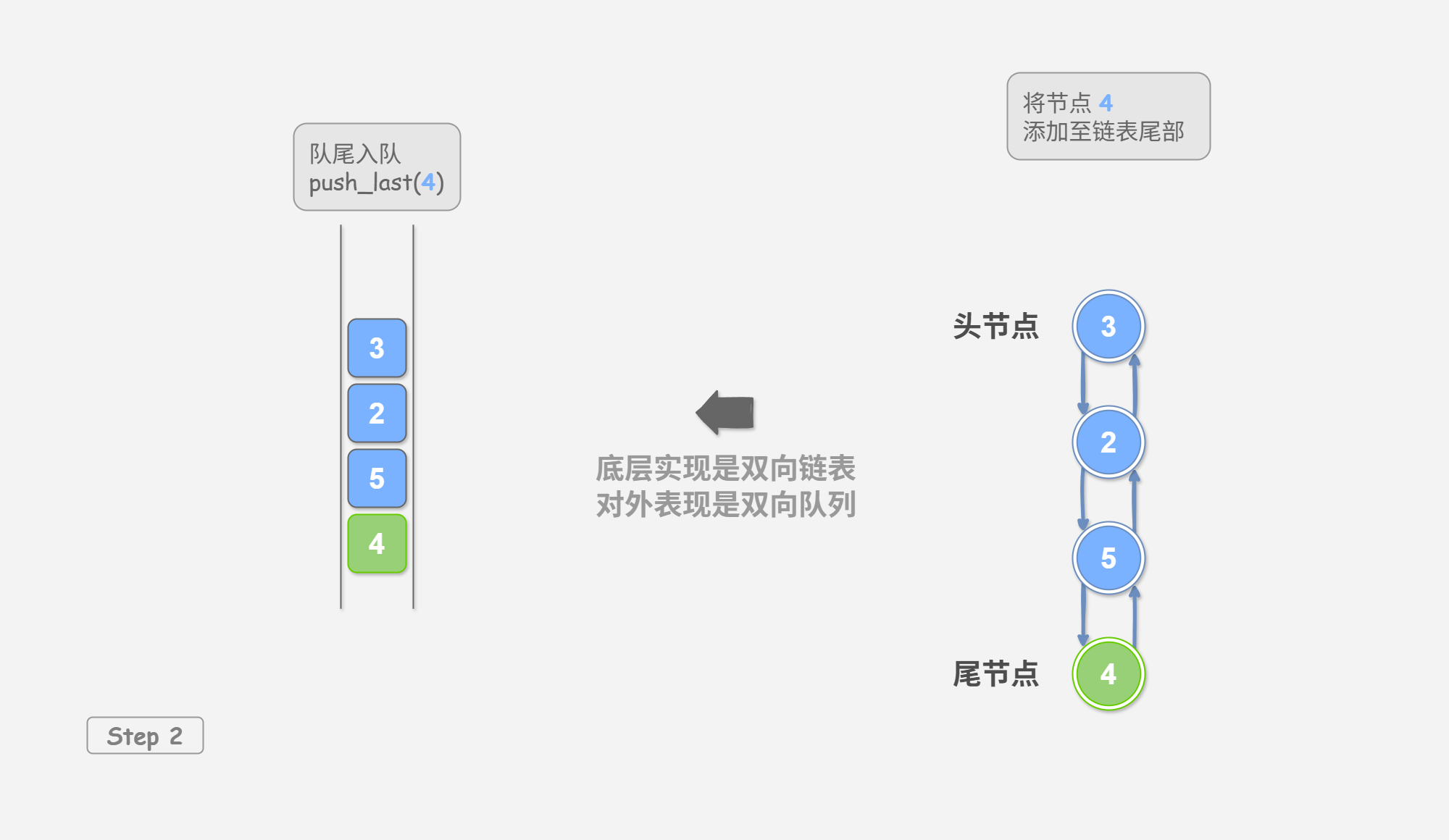
push_last()	将元素添加至队尾	$O(1)$
pop_first()	删除队首元素	$O(1)$
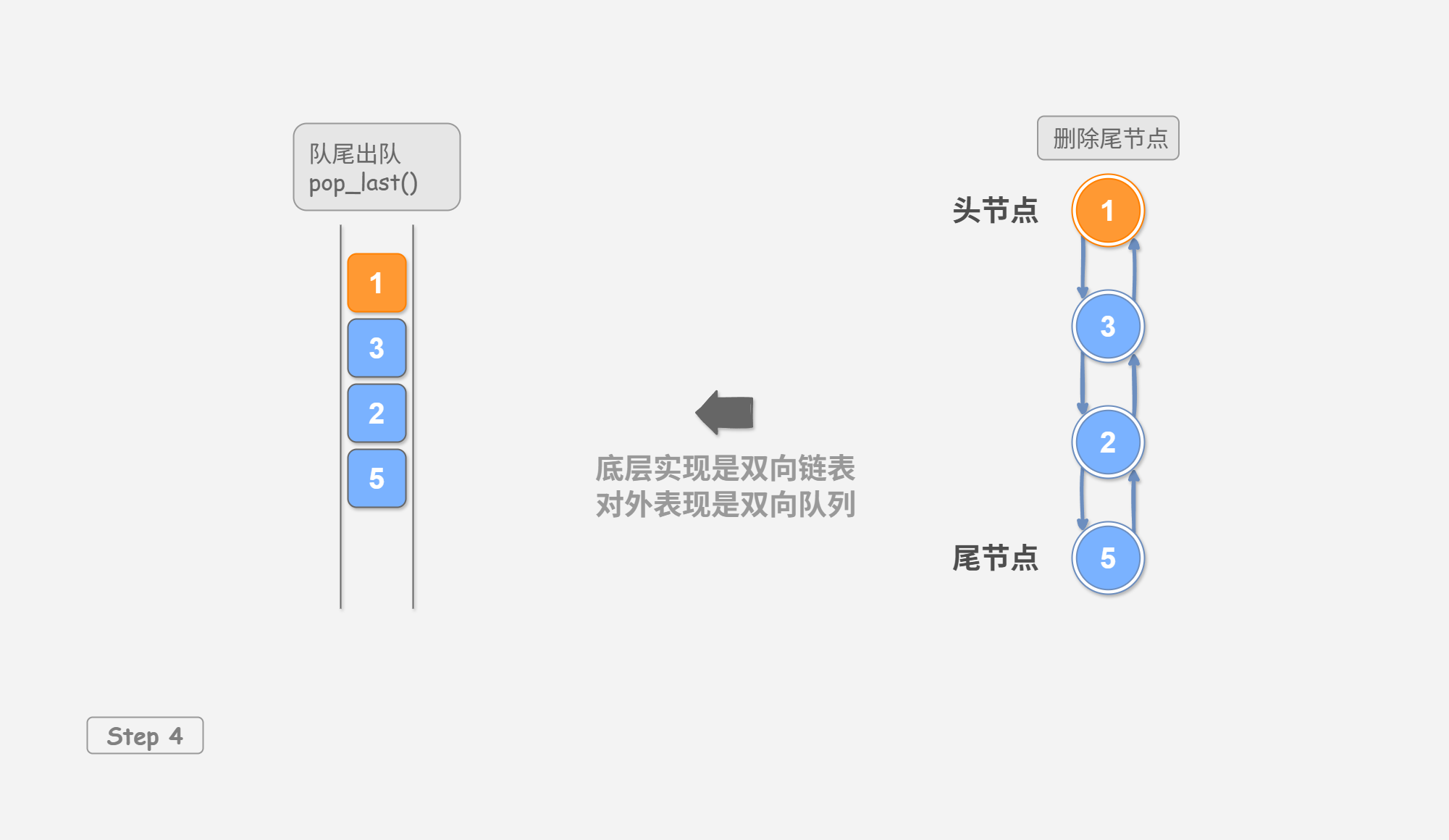
pop_last()	删除队尾元素	$O(1)$
peek_first()	访问队首元素	$O(1)$
peek_last()	访问队尾元素	$O(1)$

同样地，我们可以直接使用编程语言中以实现的双向队列类：

1	// C 未提供内置双向队列

from collections import deque

# 初始化双向队列
deq: deque[int] = deque()

# 元素入队
deq.append(2)      # 添加至队尾
deq.append(5)
deq.append(4)
deq.appendleft(3)  # 添加至队首
deq.appendleft(1)

# 访问元素
front: int = deq[0]  # 队首元素
rear: int = deq[-1]  # 队尾元素

# 元素出队
pop_front: int = deq.popleft()  # 队首元素出队
pop_rear: int = deq.pop()       # 队尾元素出队

# 获取双向队列的长度
size: int = len(deq)

# 判断双向队列是否为空
is_empty: bool = len(deq) == 0

4 双向队列实现

双向队列的实现与队列类似，可以选择链表或数组作为底层结构。

4.1 基于双向链表的实现

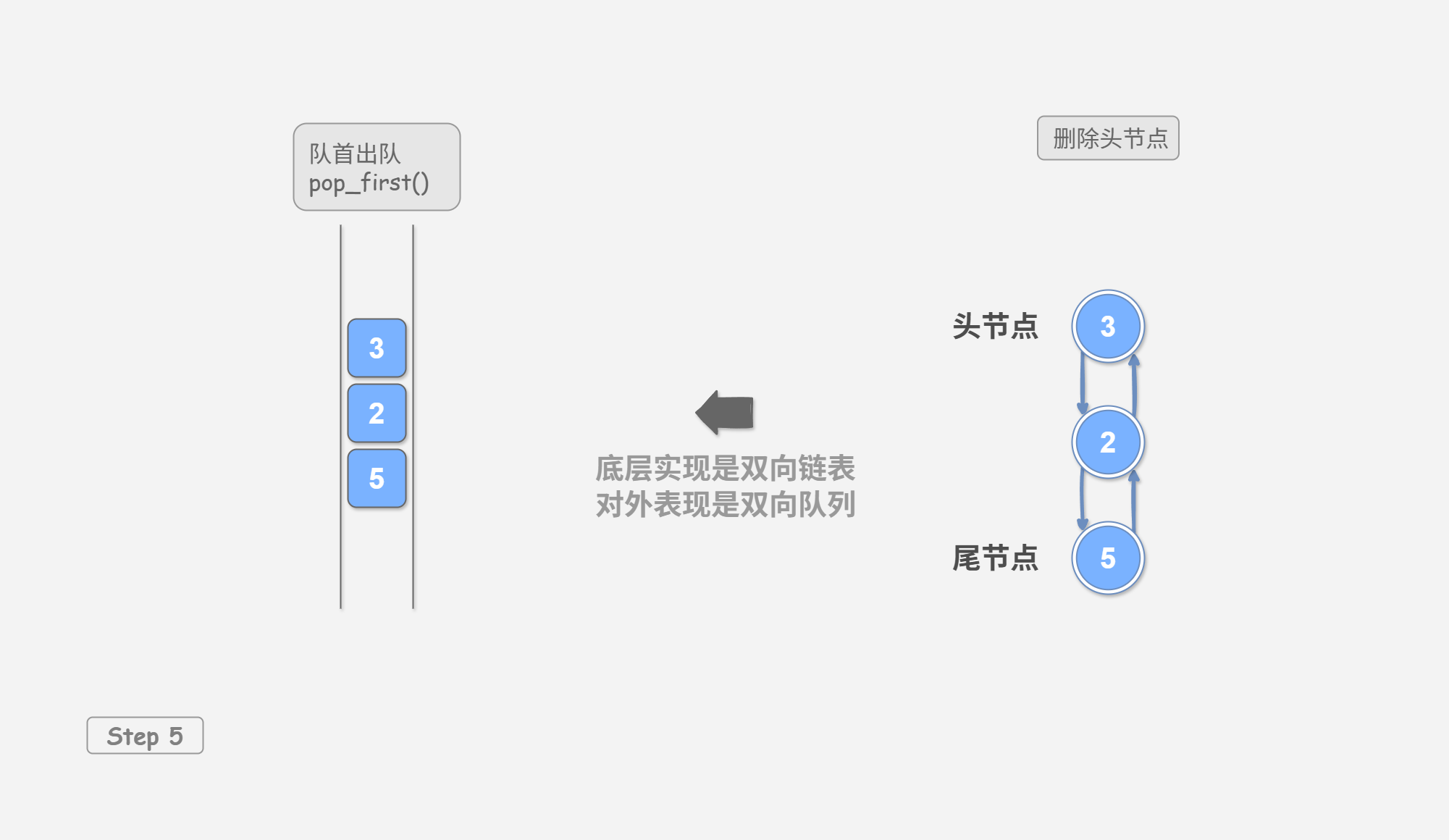
在队列中我们使用普通单向链表来实现队列，因为它可以方便地删除头节点（对应出队操作）和在尾节点后添加新节点（对应入队操作）。

对于双向队列而言，头部和尾部都可以执行入队和出队操作。换句话说，双向队列需要实现另一个对称方向的操作。为此，我们采用“双向链表”作为双向队列的底层数据结构。

如 图 4-1 所示，我们将双向链表的头节点和尾节点视为双向队列的队首和队尾，同时实现在两端添加和删除节点的功能。

图 4-1 基于链表实现双向队列的入队出队操作

实现代码如下所示：

Python

/* 双向链表节点 */
typedef struct DoublyListNode {
    int val;                     // 节点值
    struct DoublyListNode *next; // 后继节点
    struct DoublyListNode *prev; // 前驱节点
} DoublyListNode;

/* 构造函数 */
DoublyListNode *newDoublyListNode(int num) {
    DoublyListNode *new = (DoublyListNode *)malloc(sizeof(DoublyListNode));
    new->val = num;
    new->next = NULL;
    new->prev = NULL;
    return new;
}

/* 析构函数 */
void delDoublyListNode(DoublyListNode *node) {
    free(node);
}

/* 基于双向链表实现的双向队列 */
typedef struct {
    DoublyListNode *front, *rear; // 头节点 front ，尾节点 rear
    int queSize;                  // 双向队列的长度
} LinkedListDeque;

/* 构造函数 */
LinkedListDeque *newLinkedListDeque() {
    LinkedListDeque *deque = (LinkedListDeque *)malloc(sizeof(LinkedListDeque));
    deque->front = NULL;
    deque->rear = NULL;
    deque->queSize = 0;
    return deque;
}

/* 析构函数 */
void delLinkedListdeque(LinkedListDeque *deque) {
    // 释放所有节点
    for (int i = 0; i < deque->queSize && deque->front != NULL; i++) {
        DoublyListNode *tmp = deque->front;
        deque->front = deque->front->next;
        free(tmp);
    }
    // 释放 deque 结构体
    free(deque);
}

/* 获取队列的长度 */
int size(LinkedListDeque *deque) {
    return deque->queSize;
}

/* 判断队列是否为空 */
bool empty(LinkedListDeque *deque) {
    return (size(deque) == 0);
}

/* 入队 */
void push(LinkedListDeque *deque, int num, bool isFront) {
    DoublyListNode *node = newDoublyListNode(num);
    // 若链表为空，则令 front 和 rear 都指向node
    if (empty(deque)) {
        deque->front = deque->rear = node;
    }
    // 队首入队操作
    else if (isFront) {
        // 将 node 添加至链表头部
        deque->front->prev = node;
        node->next = deque->front;
        deque->front = node; // 更新头节点
    }
    // 队尾入队操作
    else {
        // 将 node 添加至链表尾部
        deque->rear->next = node;
        node->prev = deque->rear;
        deque->rear = node;
    }
    deque->queSize++; // 更新队列长度
}

/* 队首入队 */
void pushFirst(LinkedListDeque *deque, int num) {
    push(deque, num, true);
}

/* 队尾入队 */
void pushLast(LinkedListDeque *deque, int num) {
    push(deque, num, false);
}

/* 访问队首元素 */
int peekFirst(LinkedListDeque *deque) {
    assert(size(deque) && deque->front);
    return deque->front->val;
}

/* 访问队尾元素 */
int peekLast(LinkedListDeque *deque) {
    assert(size(deque) && deque->rear);
    return deque->rear->val;
}

/* 出队 */
int pop(LinkedListDeque *deque, bool isFront) {
    if (empty(deque))
        return -1;
    int val;
    // 队首出队操作
    if (isFront) {
        val = peekFirst(deque); // 暂存头节点值
        DoublyListNode *fNext = deque->front->next;
        if (fNext) {
            fNext->prev = NULL;
            deque->front->next = NULL;
        }
        delDoublyListNode(deque->front);
        deque->front = fNext; // 更新头节点
    }
    // 队尾出队操作
    else {
        val = peekLast(deque); // 暂存尾节点值
        DoublyListNode *rPrev = deque->rear->prev;
        if (rPrev) {
            rPrev->next = NULL;
            deque->rear->prev = NULL;
        }
        delDoublyListNode(deque->rear);
        deque->rear = rPrev; // 更新尾节点
    }
    deque->queSize--; // 更新队列长度
    return val;
}

/* 队首出队 */
int popFirst(LinkedListDeque *deque) {
    return pop(deque, true);
}

/* 队尾出队 */
int popLast(LinkedListDeque *deque) {
    return pop(deque, false);
}

/* 打印队列 */
void printLinkedListDeque(LinkedListDeque *deque) {
    int *arr = malloc(sizeof(int) * deque->queSize);
    // 拷贝链表中的数据到数组
    int i;
    DoublyListNode *node;
    for (i = 0, node = deque->front; i < deque->queSize; i++) {
        arr[i] = node->val;
        node = node->next;
    }
    printArray(arr, deque->queSize);
    free(arr);
}

class ListNode:
    """双向链表节点"""

    def __init__(self, val: int):
        """构造方法"""
        self.val: int = val
        self.next: ListNode | None = None  # 后继节点引用
        self.prev: ListNode | None = None  # 前驱节点引用

class LinkedListDeque:
    """基于双向链表实现的双向队列"""

    def __init__(self):
        """构造方法"""
        self._front: ListNode | None = None  # 头节点 front
        self._rear: ListNode | None = None  # 尾节点 rear
        self._size: int = 0  # 双向队列的长度

    def size(self) -> int:
        """获取双向队列的长度"""
        return self._size

    def is_empty(self) -> bool:
        """判断双向队列是否为空"""
        return self._size == 0

    def push(self, num: int, is_front: bool):
        """入队操作"""
        node = ListNode(num)
        # 若链表为空，则令 front 和 rear 都指向 node
        if self.is_empty():
            self._front = self._rear = node
        # 队首入队操作
        elif is_front:
            # 将 node 添加至链表头部
            self._front.prev = node
            node.next = self._front
            self._front = node  # 更新头节点
        # 队尾入队操作
        else:
            # 将 node 添加至链表尾部
            self._rear.next = node
            node.prev = self._rear
            self._rear = node  # 更新尾节点
        self._size += 1  # 更新队列长度

    def push_first(self, num: int):
        """队首入队"""
        self.push(num, True)

    def push_last(self, num: int):
        """队尾入队"""
        self.push(num, False)

    def pop(self, is_front: bool) -> int:
        """出队操作"""
        if self.is_empty():
            raise IndexError("双向队列为空")
        # 队首出队操作
        if is_front:
            val: int = self._front.val  # 暂存头节点值
            # 删除头节点
            fnext: ListNode | None = self._front.next
            if fnext is not None:
                fnext.prev = None
                self._front.next = None
            self._front = fnext  # 更新头节点
        # 队尾出队操作
        else:
            val: int = self._rear.val  # 暂存尾节点值
            # 删除尾节点
            rprev: ListNode | None = self._rear.prev
            if rprev is not None:
                rprev.next = None
                self._rear.prev = None
            self._rear = rprev  # 更新尾节点
        self._size -= 1  # 更新队列长度
        return val

    def pop_first(self) -> int:
        """队首出队"""
        return self.pop(True)

    def pop_last(self) -> int:
        """队尾出队"""
        return self.pop(False)

    def peek_first(self) -> int:
        """访问队首元素"""
        if self.is_empty():
            raise IndexError("双向队列为空")
        return self._front.val

    def peek_last(self) -> int:
        """访问队尾元素"""
        if self.is_empty():
            raise IndexError("双向队列为空")
        return self._rear.val

    def to_array(self) -> list[int]:
        """返回数组用于打印"""
        node = self._front
        res = [0] * self.size()
        for i in range(self.size()):
            res[i] = node.val
            node = node.next
        return res

4.2 基于数组的实现

如 图 4-2 所示，与基于数组实现队列类似，我们也可以使用环形数组来实现双向队列。

图 4-2 基于数组实现双向队列的入队出队操作

在队列的实现基础上，仅需增加 “队首入队” 和 “队尾出队” 的方法：

Python

/* 基于环形数组实现的双向队列 */
typedef struct {
    int *nums;       // 用于存储队列元素的数组
    int front;       // 队首指针，指向队首元素
    int queSize;     // 尾指针，指向队尾 + 1
    int queCapacity; // 队列容量
} ArrayDeque;

/* 构造函数 */
ArrayDeque *newArrayDeque(int capacity) {
    ArrayDeque *deque = (ArrayDeque *)malloc(sizeof(ArrayDeque));
    // 初始化数组
    deque->queCapacity = capacity;
    deque->nums = (int *)malloc(sizeof(int) * deque->queCapacity);
    deque->front = deque->queSize = 0;
    return deque;
}

/* 析构函数 */
void delArrayDeque(ArrayDeque *deque) {
    free(deque->nums);
    free(deque);
}

/* 获取双向队列的容量 */
int capacity(ArrayDeque *deque) {
    return deque->queCapacity;
}

/* 获取双向队列的长度 */
int size(ArrayDeque *deque) {
    return deque->queSize;
}

/* 判断双向队列是否为空 */
bool empty(ArrayDeque *deque) {
    return deque->queSize == 0;
}

/* 计算环形数组索引 */
int dequeIndex(ArrayDeque *deque, int i) {
    // 通过取余操作实现数组首尾相连
    // 当 i 越过数组尾部时，回到头部
    // 当 i 越过数组头部后，回到尾部
    return ((i + capacity(deque)) % capacity(deque));
}

/* 队首入队 */
void pushFirst(ArrayDeque *deque, int num) {
    if (deque->queSize == capacity(deque)) {
        printf("双向队列已满\r\n");
        return;
    }
    // 队首指针向左移动一位
    // 通过取余操作实现 front 越过数组头部回到尾部
    deque->front = dequeIndex(deque, deque->front - 1);
    // 将 num 添加到队首
    deque->nums[deque->front] = num;
    deque->queSize++;
}

/* 队尾入队 */
void pushLast(ArrayDeque *deque, int num) {
    if (deque->queSize == capacity(deque)) {
        printf("双向队列已满\r\n");
        return;
    }
    // 计算队尾指针，指向队尾索引 + 1
    int rear = dequeIndex(deque, deque->front + deque->queSize);
    // 将 num 添加至队尾
    deque->nums[rear] = num;
    deque->queSize++;
}

/* 访问队首元素 */
int peekFirst(ArrayDeque *deque) {
    // 访问异常：双向队列为空
    assert(empty(deque) == 0);
    return deque->nums[deque->front];
}

/* 访问队尾元素 */
int peekLast(ArrayDeque *deque) {
    // 访问异常：双向队列为空
    assert(empty(deque) == 0);
    int last = dequeIndex(deque, deque->front + deque->queSize - 1);
    return deque->nums[last];
}

/* 队首出队 */
int popFirst(ArrayDeque *deque) {
    int num = peekFirst(deque);
    // 队首指针向后移动一位
    deque->front = dequeIndex(deque, deque->front + 1);
    deque->queSize--;
    return num;
}

/* 队尾出队 */
int popLast(ArrayDeque *deque) {
    int num = peekLast(deque);
    deque->queSize--;
    return num;
}

/* 返回数组用于打印 */
int *toArray(ArrayDeque *deque, int *queSize) {
    *queSize = deque->queSize;
    int *res = (int *)calloc(deque->queSize, sizeof(int));
    int j = deque->front;
    for (int i = 0; i < deque->queSize; i++) {
        res[i] = deque->nums[j % deque->queCapacity];
        j++;
    }
    return res;
}

class ArrayDeque:
    """基于环形数组实现的双向队列"""

    def __init__(self, capacity: int):
        """构造方法"""
        self._nums: list[int] = [0] * capacity
        self._front: int = 0
        self._size: int = 0

    def capacity(self) -> int:
        """获取双向队列的容量"""
        return len(self._nums)

    def size(self) -> int:
        """获取双向队列的长度"""
        return self._size

    def is_empty(self) -> bool:
        """判断双向队列是否为空"""
        return self._size == 0

    def index(self, i: int) -> int:
        """计算环形数组索引"""
        # 通过取余操作实现数组首尾相连
        # 当 i 越过数组尾部后，回到头部
        # 当 i 越过数组头部后，回到尾部
        return (i + self.capacity()) % self.capacity()

    def push_first(self, num: int):
        """队首入队"""
        if self._size == self.capacity():
            print("双向队列已满")
            return
        # 队首指针向左移动一位
        # 通过取余操作实现 front 越过数组头部后回到尾部
        self._front = self.index(self._front - 1)
        # 将 num 添加至队首
        self._nums[self._front] = num
        self._size += 1

    def push_last(self, num: int):
        """队尾入队"""
        if self._size == self.capacity():
            print("双向队列已满")
            return
        # 计算队尾指针，指向队尾索引 + 1
        rear = self.index(self._front + self._size)
        # 将 num 添加至队尾
        self._nums[rear] = num
        self._size += 1

    def pop_first(self) -> int:
        """队首出队"""
        num = self.peek_first()
        # 队首指针向后移动一位
        self._front = self.index(self._front + 1)
        self._size -= 1
        return num

    def pop_last(self) -> int:
        """队尾出队"""
        num = self.peek_last()
        self._size -= 1
        return num

    def peek_first(self) -> int:
        """访问队首元素"""
        if self.is_empty():
            raise IndexError("双向队列为空")
        return self._nums[self._front]

    def peek_last(self) -> int:
        """访问队尾元素"""
        if self.is_empty():
            raise IndexError("双向队列为空")
        # 计算尾元素索引
        last = self.index(self._front + self._size - 1)
        return self._nums[last]

    def to_array(self) -> list[int]:
        """返回数组用于打印"""
        # 仅转换有效长度范围内的列表元素
        res = []
        for i in range(self._size):
            res.append(self._nums[self.index(self._front + i)])
        return res

5 典型应用

5.1 队列

淘宝订单： 购物者下单后，订单将加入队列中，系统随后会根据顺序处理队列中的订单。在双十一期间，短时间内会产生海量订单，高并发成为工程师们需要重点攻克的问题。
各类待办事项： 任何需要实现“先来后到”功能的场景，例如打印机的任务队列、餐厅的出餐队列等，队列在这些场景中可以有效地维护处理顺序。

5.2 双向队列应用

双向队列兼具栈与队列的逻辑，因此它可以实现这两者的所有应用场景，同时提供更高的自由度。

我们知道，软件的“撤销”功能通常使用栈来实现：系统将每次更改操作 push 到栈中，然后通过 pop 实现撤销。然而，考虑到系统资源的限制，软件通常会限制撤销的步数（例如仅允许保存 50 步）。当栈的长度超过 50 时，软件需要在栈底（队首）执行删除操作。但栈无法实现该功能，此时就需要使用双向队列来替代栈。请注意，“撤销”的核心逻辑仍然遵循栈的先入后出原则，只是双向队列能够更加灵活地实现一些额外逻辑。

本文采用署名-非商业性使用-相同方式共享 4.0 国际许可协议，转载请注明出处。