数据结构 - 线性结构 - 链表(Linked List)

1 概念

内存空间是所有程序的公共资源，在一个复杂的系统运行环境下，空闲的内存空间可能散落在内存各处。我们知道，存储数组的内存空间必须是连续的，而当数据非常大时，内存可能无法提供如此大的连续空间。此时链表的灵活性优势就体现出来了。

链表 (Linked List) 是一种线性数据结构，其中的每个元素都是一个节点对象，各个节点通过“引用”相连接。引用记录了下一个节点的内存地址，通过它可以从当前节点访问到下一个节点。

链表的设计使得各个节点可以分散存储在内存各处，他们的内存地址无须连续。

图 1-1 链表定义与存储方式

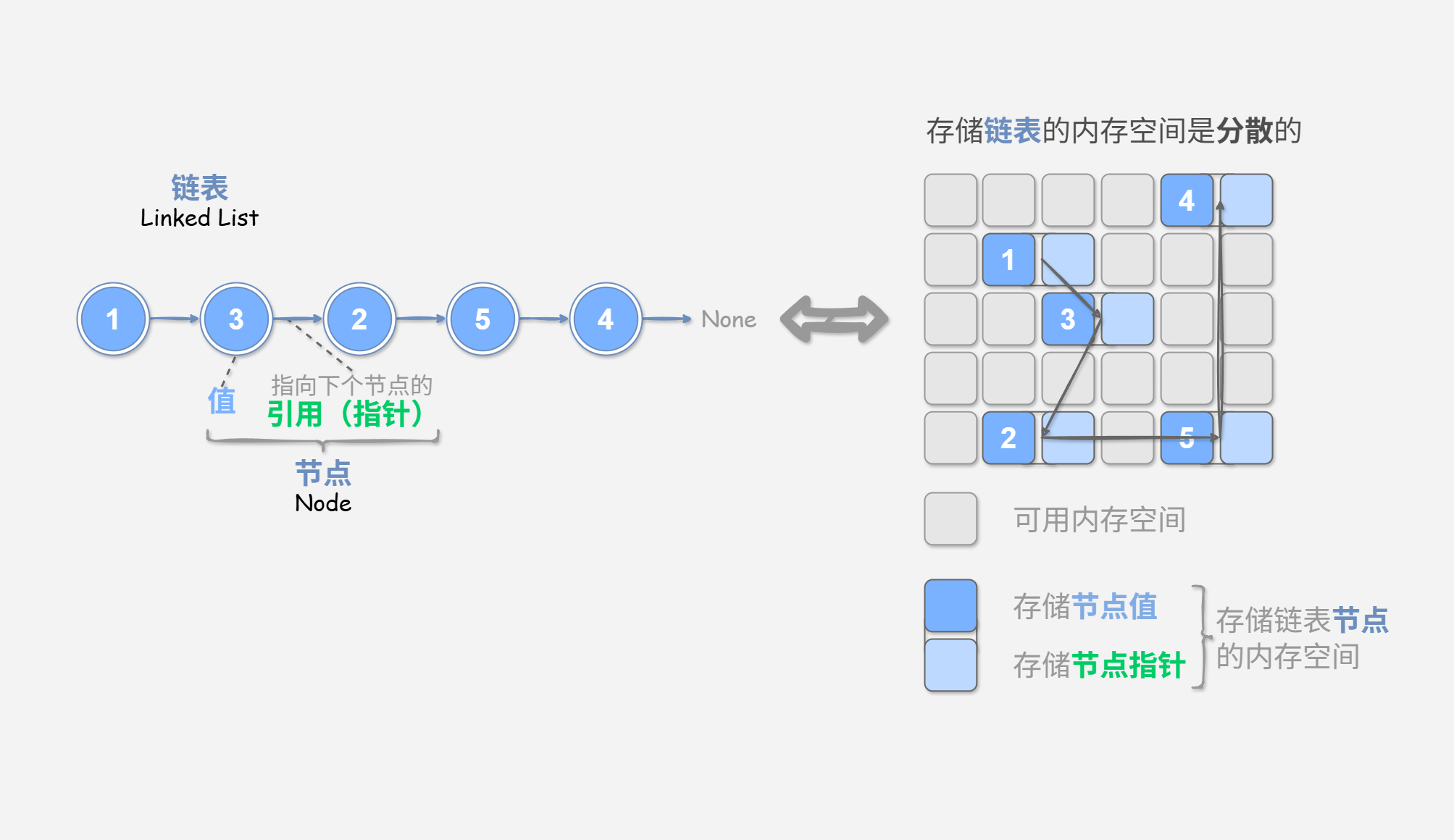
观察 图 1-1 ，链表的组成单位是节点 (node) 对象。每个节点都包含两项数据：节点的“值”和指向下一节点的“引用”。

• 链表的首个节点被称为“头节点”，最后一个节点被成为“尾节点”。
• 尾节点指向的是“空”，它在 Java 、 C++ 和 Python 中分别被记为 null 、 nullptr 和 None 。
• 在 C 、 C++ 、 Go 和 Rust 等支持指针的语言中，上述“引用”应被替换为“指针”。

如以下代码所示，链表节点 ListNode 除了包含值，还需额外保存一个引用（指针）。因此在相同数量下，链表比数组占用更多的内存空间。

1
2
3
4
5
6
7
8
9
10
11
12
13
14

/* 链表节点结构体 */
typedef struct ListNode {
    int val;               // 节点值
    struct ListNode *next; // 指向下一节点的指针
} ListNode;

/* 构造函数 */
ListNode *newListNode(int val) {
    ListNode *node;
    node = (ListNode *) malloc(sizeof(ListNode));
    node->val = val;
    node->next = NULL;
    return node;
}

1
2
3
4
5

class ListNode:
    """链表节点类"""
    def __init__(self, val: int):
        self.val: int = val               # 节点值
        self.next: ListNode | None = None # 指向下一节点的引用

2 链表常用操作

2.1 初始化链表

建立链表分为两步，第一步是初始化各个节点对象，第二步是构建节点之间的引用关系。初始化完成后，我们就可以从链表的头节点出发，通过引用指向 next 依次访问所有节点。

1
2
3
4
5
6
7
8
9
10
11
12

/* 初始化链表 1 -> 3 -> 2 -> 5 -> 4 */
// 初始化各个节点
ListNode* n0 = newListNode(1);
ListNode* n1 = newListNode(3);
ListNode* n2 = newListNode(2);
ListNode* n3 = newListNode(5);
ListNode* n4 = newListNode(4);
// 构建节点之间的引用
n0->next = n1;
n1->next = n2;
n2->next = n3;
n3->next = n4;

1
2
3
4
5
6
7
8
9
10
11
12

# 初始化链表 1 -> 3 -> 2 -> 5 -> 4
# 初始化各个节点
n0 = ListNode(1)
n1 = ListNode(3)
n2 = ListNode(2)
n3 = ListNode(5)
n4 = ListNode(4)
# 构建节点之间的引用
n0.next = n1
n1.next = n2
n2.next = n3
n3.next = n4

数组整体是一个变量，比如数组 nums 包含元素 nums[0] 和 num[1] 等，而链表是有多个独立的节点对象组成的。我们通常将头节点当作链表的代称，比如以上代码中的链表可以记作链表 n0 。

2.2 插入节点

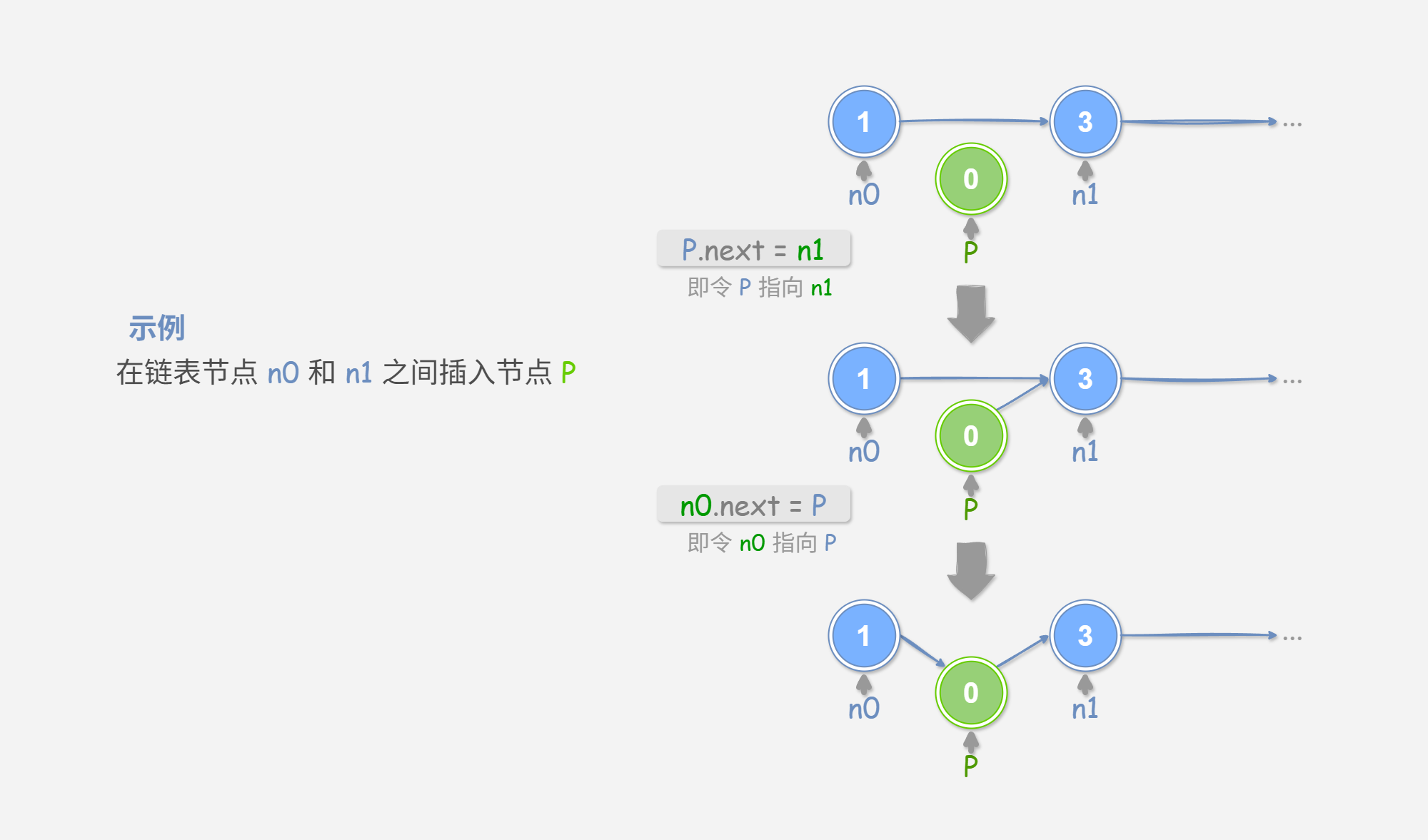
在链表中插入节点非常容易。如 图 2-1 所示，假设我们想在相邻的两个节点 n0 和 n1 之间插入一个新节点 P ，则只需改变两个节点引用（指针）即可，时间复杂度为 O(1) 。

相比之下，在数组中插入元素的时间复杂度为 O(n) ，在大数据量下的效率低。

图 2-1 链表插入节点示例

1
2
3
4
5
6

/* 在链表的节点 n0 之后插入节点 P */
void insert(ListNode *n0, ListNode *P) {
    ListNode *n1 = n0->next;
    P->next = n1;
    n0->next = P;
}

1
2
3
4
5

def insert(n0: ListNode, P: ListNode):
    """在链表的节点 n0 之后插入节点 P"""
    n1 = n0.next
    P.next = n1
    n0.next = P

2.3 删除节点

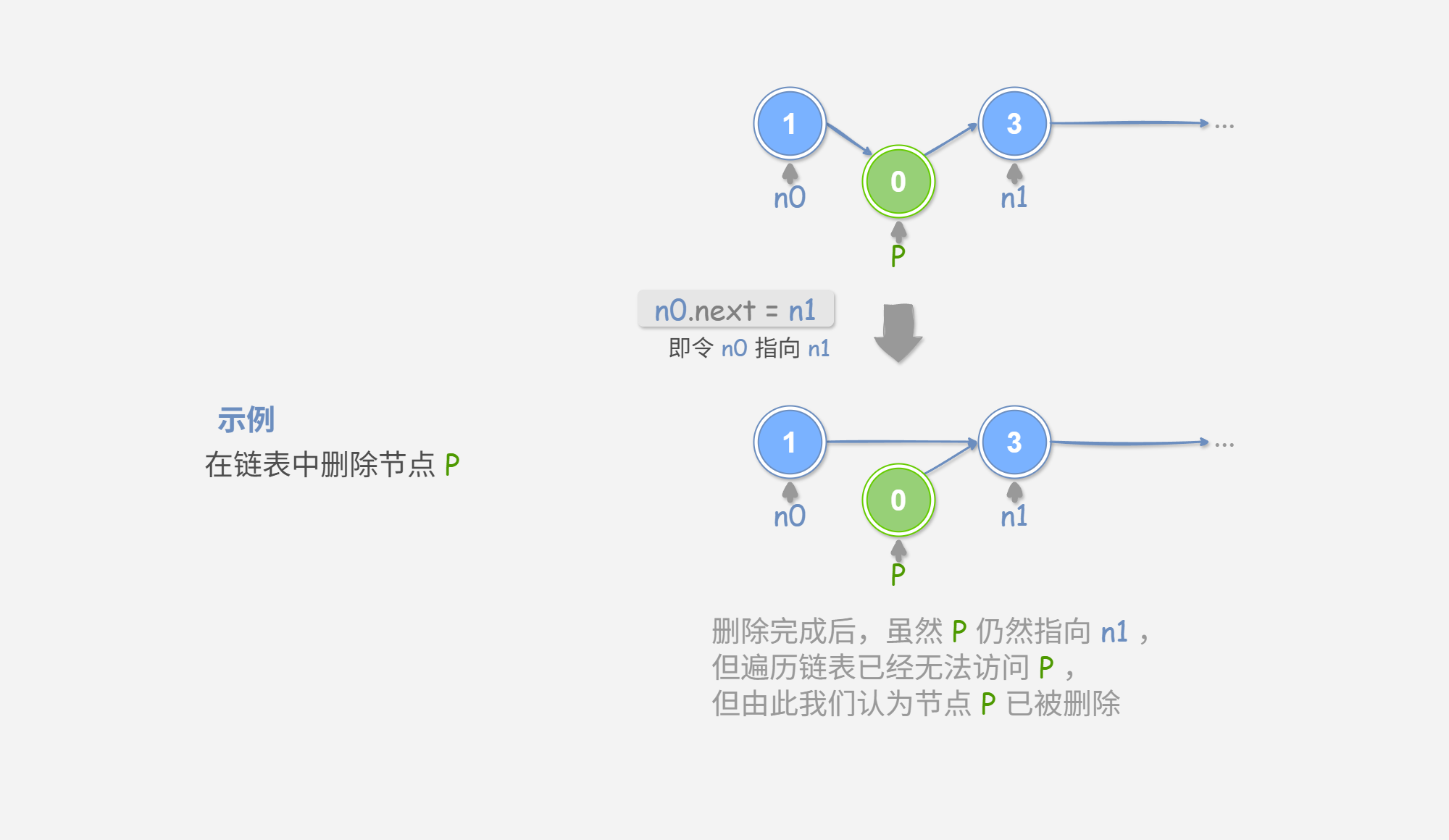
如 图 2-2 所示，在链表中删除节点也非常方便，只需改变一个结点的引用（指针）即可。

请注意，尽管在删除操作完成后节点 P 仍然指向 n1 ，但实际上遍历此链表已经无法访问到 P ，这意味着 P 已经不再属于该链表了。

图 2-2 链表删除节点示例

1
2
3
4
5
6
7
8
9
10
11
12

/* 删除链表的节点 n0 之后的首个节点 */
// 注意：stdio.h 占用了 remove 关键词
void removeItem(ListNode *n0) {
    if (!n0->next)
        return;
    // n0 -> P -> n1
    ListNode *P = n0->next;
    ListNode *n1 = P->next;
    n0->next = n1;
    // 释放内存
    free(P);
}

1
2
3
4
5
6
7
8

def remove(n0: ListNode):
    """删除链表的节点 n0 之后的首个节点"""
    if not n0.next:
        return
    # n0 -> P -> n1
    P = n0.next
    n1 = P.next
    n0.next = n1

2.4 访问节点

在链表中访问节点的效率较低。如上一节所述，我们可以在 O(1) 时间下访问数组中的任意元素。链表则不然，程序需要从头节点出发，逐个向后遍历，直至找到目标节点。也就是说，访问链表的第 i 个节点需要循环 i-1 轮，时间复杂度为 O(n) 。

1
2
3
4
5
6
7
8
9

/* 访问链表中索引为 index 的节点 */
ListNode *access(ListNode *head, int index) {
    for (int i = 0; i < index; i++) {
        if (head == NULL)
            return NULL;
        head = head->next;
    }
    return head;
}

1
2
3
4
5
6
7

def access(head: ListNode, index: int) -> ListNode | None:
    """访问链表中索引为 index 的节点"""
    for _ in range(index):
        if not head:
            return None
        head = head.next
    return head

2.5 查找结点

遍历链表，查找其中值为 target 的节点，输出改节点在链表中的索引。此过程也属于线性查找。代码如下所示：

1
2
3
4
5
6
7
8
9
10
11

/* 在链表中查找值为 target 的首个节点 */
int find(ListNode *head, int target) {
    int index = 0;
    while (head) {
        if (head->val == target)
            return index;
        head = head->next;
        index++;
    }
    return -1;
}

1
2
3
4
5
6
7
8
9

def find(head: ListNode, target: int) -> int:
    """在链表中查找值为 target 的首个节点"""
    index = 0
    while head:
        if head.val == target:
            return index
        head = head.next
        index += 1
    return -1

3 数组 VS 链表

下表总结了数组和链表的各项特点并对比了操作效率。由于他们采用两种相反的存储策略，因此各种性质和操作效率也呈现对立的特点。

4 常见链表类型

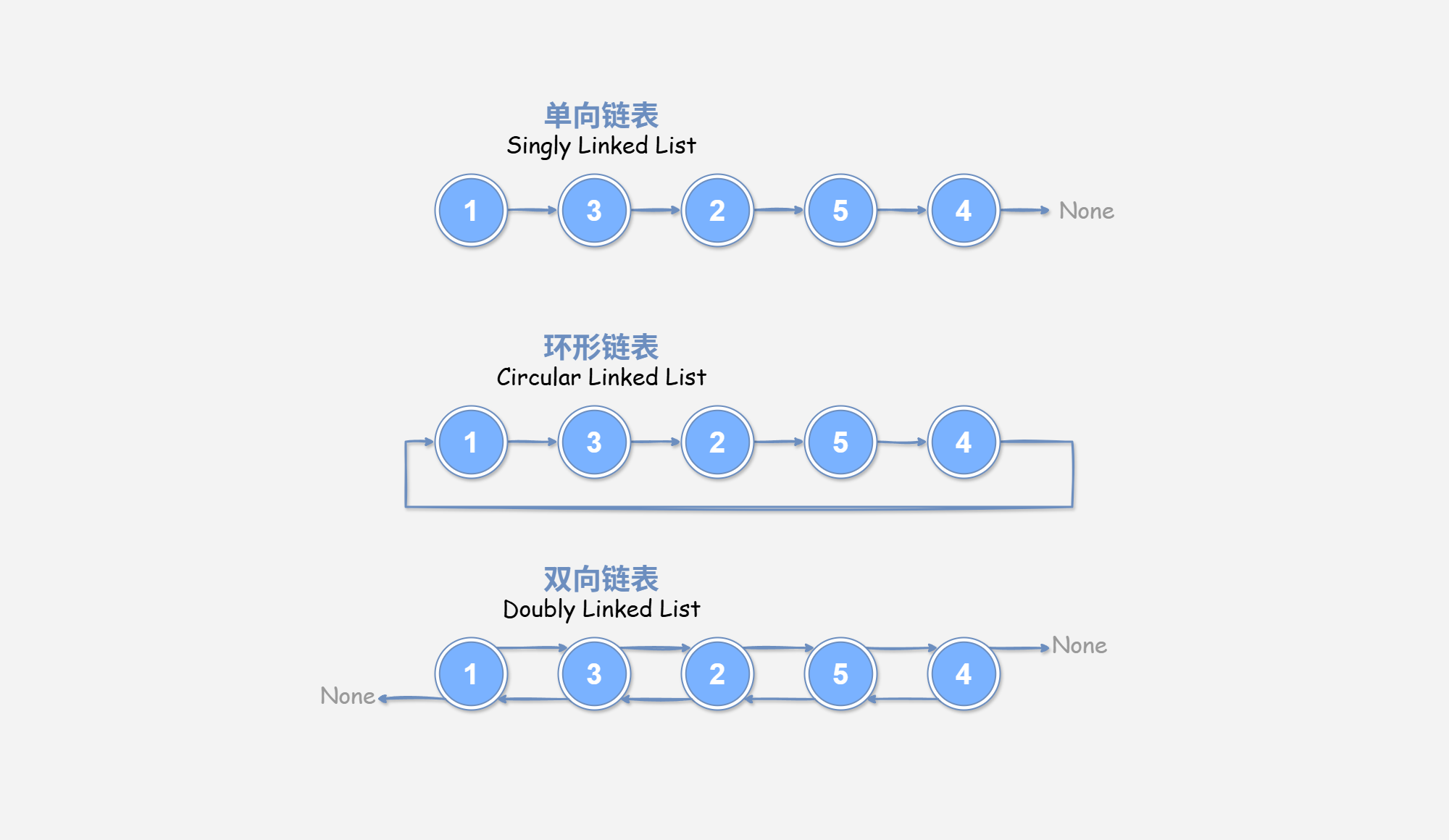
如 图 4-1 所示，常见的链表类型包括三种：

• 单向链表： 即前面介绍的普通链表。单向链表的节点包含值和指向下一节点的引用两项数据。我们将首个节点成为头节点，将最后一个节点成为尾节点，尾节点指向空 None 。
• 环形链表： 如果我们令单向链表的尾节点指向头节点（首尾相接），则得到一个环形链表。在环形链表中，任意节点都可以视作头节点。
• 双向链表： 与单链表相比，双向链表记录了两个方向的引用。双向链表的节点定义同时包含指向后继节点（下一个节点）和前驱节点（上一个节点）的引用（指针）。相较于单向链表，双向链表更具灵活性，可以朝两个方向遍历链表，但相应地也需要占用更多的内存空间。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

/* 双向链表节点结构体 */
typedef struct ListNode {
    int val;               // 节点值
    struct ListNode *next; // 指向后继节点的指针
    struct ListNode *prev; // 指向前驱节点的指针
} ListNode;

/* 构造函数 */
ListNode *newListNode(int val) {
    ListNode *node;
    node = (ListNode *) malloc(sizeof(ListNode));
    node->val = val;
    node->next = NULL;
    node->prev = NULL;
    return node;
}

1
2
3
4
5
6

class ListNode:
    """双向链表节点类"""
    def __init__(self, val: int):
        self.val: int = val                # 节点值
        self.next: ListNode | None = None  # 指向后继节点的引用
        self.prev: ListNode | None = None  # 指向前驱节点的引用

图 4-1 链表删除节点示例

链表典型应用

单向链表通常用于实现栈、队列、哈希表和图等数据结构。

• 栈与队列： 当插入和删除操作都在链表的一端进行时，它表现的特性为先进后出，对应站；当插入操作在链表的一端进行，删除操作在链表的另一端进行，它表现的特性为先进先出，对应队列。
• 哈希表： 链式地址是解决哈希冲突的主流方案之一，在该方案中，所有冲突的元素都会被放到一个链表中。
• 图： 邻接表是表示图的一种常用方式，其中图的每个顶点都与一个链表相关联，链表中的每个元素都代表与该顶点项链的其他顶点。

双向链表常用于需要快速查找前一个和后一个元素的场景。

• 高级数据结构： 比如在红黑树、B 树中，我们需要访问节点的父节点，这可以通过在节点中保存一个指向父节点的引用来实现，类似于双向链表。
• 浏览器历史： 在网页浏览器中，当用户电机前进或后退按钮时，浏览器需要知道用户访问过的前一个和后一个网页。双向链表的特性使得这种操作变得简单。
• LRU 算法： 在缓存淘汰 (LRU) 算法中，我们需要快速找到最近最少使用的数据，以及支持快速添加和删除节点。这时候使用双向链表就非常合适。

环形链表常用于需要周期性操作的场景，比如操作系统的资源调度。

• 时间片轮转调度算法： 在操作系统中，时间片轮转调度算法是一种常见的 CPU 调度算法，它需要一组进程进行循环。每个进程被赋予一个时间片，当时间片用完时， CPU 将切换到下一个进程。这种循环操作可以通过环形链表来实现。
• 数据缓冲区： 在某些数据缓冲区的实现中，也可能会使用环形链表。比如在音频、视频播放器中，数据流可能会被分成多个缓冲块并放入一个环形链表，以便实现无缝播放。